When we do FFT to the signal to find the frequency content, the noise have an effect of getting the correct frequency. Let’s do a test this week to see what are the effects if we add in different level of noise to a signal. You can find all the code at Qingkai's Github.
import numpy as np
from scipy import fft, arange
import matplotlib.pyplot as plt
from scipy import signal
%matplotlib inline
plt.style.use('seaborn-poster')
def plotSpectrum(t, y,Fs, title = None):
"""
Function to plot the time domain and frequency domain signal
"""
n = len(y) # length of the signal
k = arange(n)
T = n/Fs
frq = k/T # two sides frequency range
frq = frq[range(n/2)] # one side frequency range
Y = fft(y)/n # fft computing and normalization
Y = Y[range(n/2)]
# plot time domain and frequency domain signal
plt.subplot(2,1,1)
plt.plot(t,y)
plt.xlabel('Time')
plt.ylabel('Amplitude')
if title:
plt.title(title)
plt.subplot(2,1,2)
plt.stem(frq,abs(Y),'r')
plt.xlabel('Freq (Hz)')
plt.ylabel('|Y(freq)|')
plt.tight_layout()
plt.show()
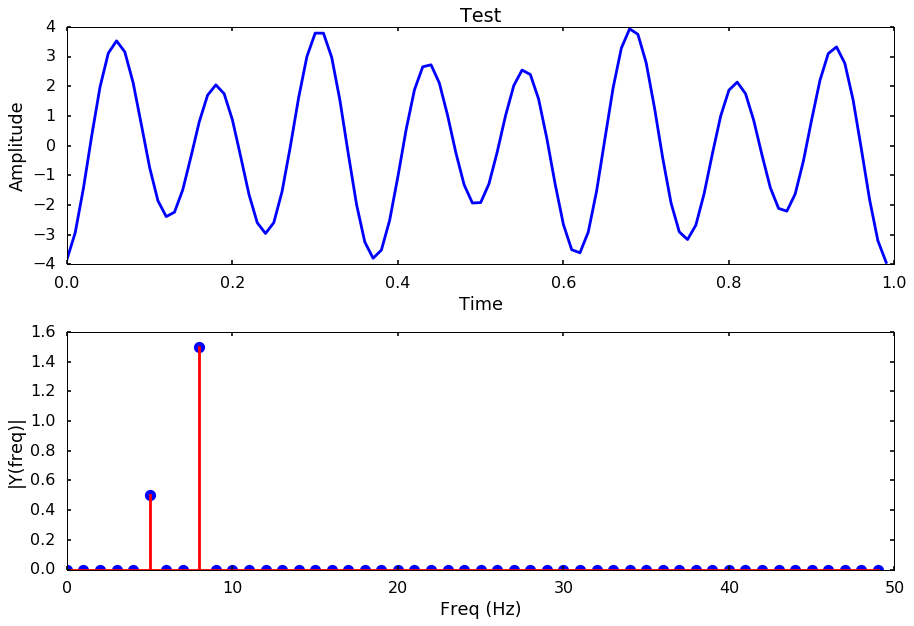
Let’s first generate a signal with two frequencies in the signal, 5 Hz and 8 Hz.
Fs = 100.0 # sampling rate
Ts = 1.0/Fs # sampling interval
t = arange(0,1,Ts) # time vector
ff_1 = 5 # frequency of the signal
ff_2 = 8
# create the signal
y = np.sin(2*np.pi*ff_1*t + 5) + 3 * np.sin(2*np.pi*ff_2*t + 5)
plotSpectrum(t, y,Fs, title = 'Test')
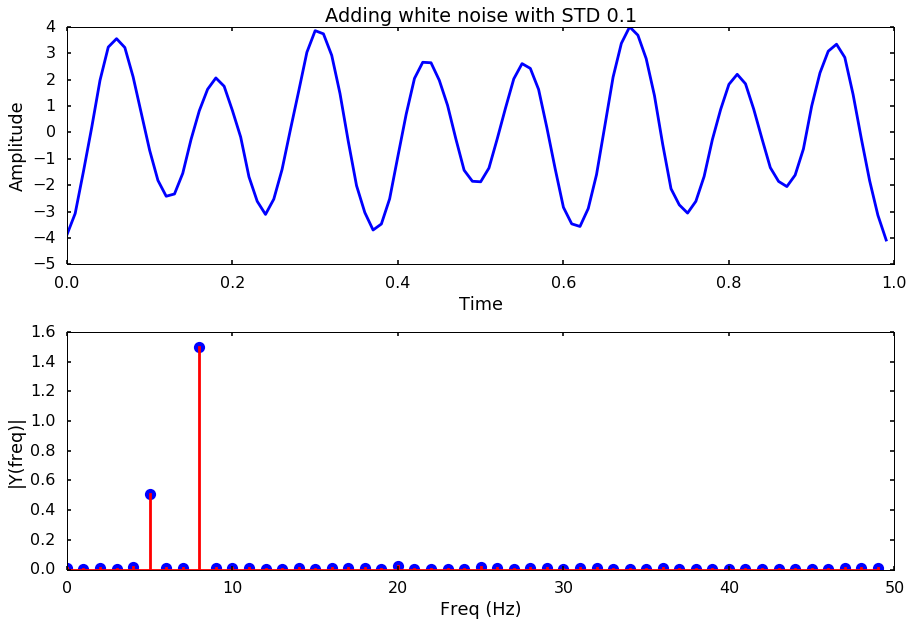
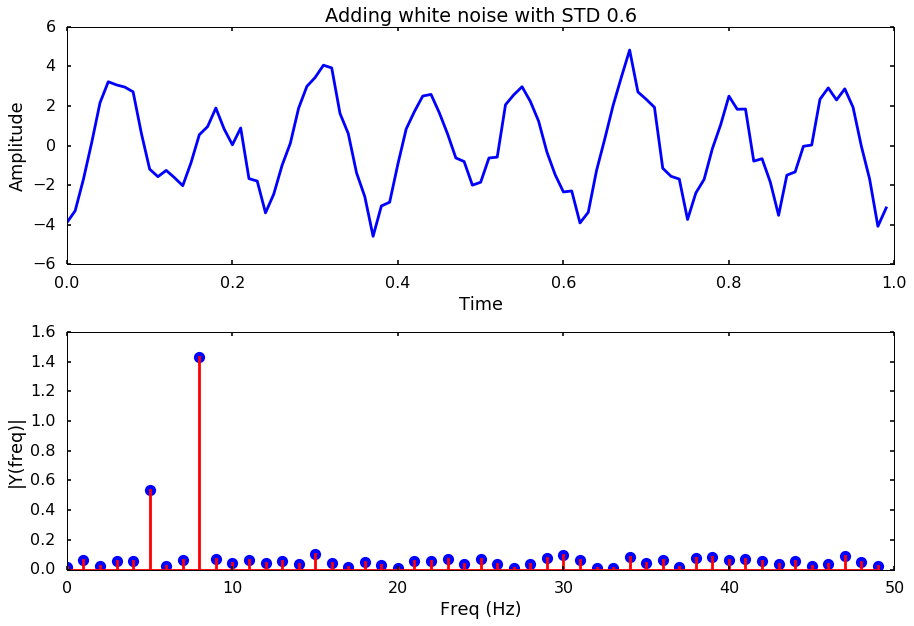
Let’s try different noise levels
for i, std_noise in enumerate(np.arange(0.1, 3, 0.5)):
title = 'Adding white noise with STD %.1f'%std_noise
noise = np.array([np.random.normal(scale=std_noise) for i in range(len(y))])
y_noise = y + noise
plotSpectrum(t, y_noise,Fs, title = title)
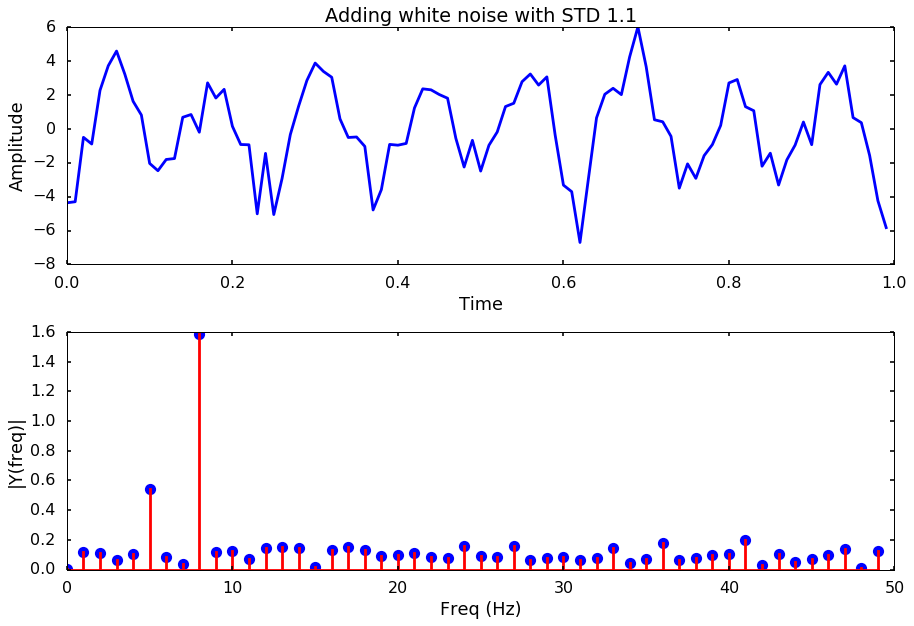
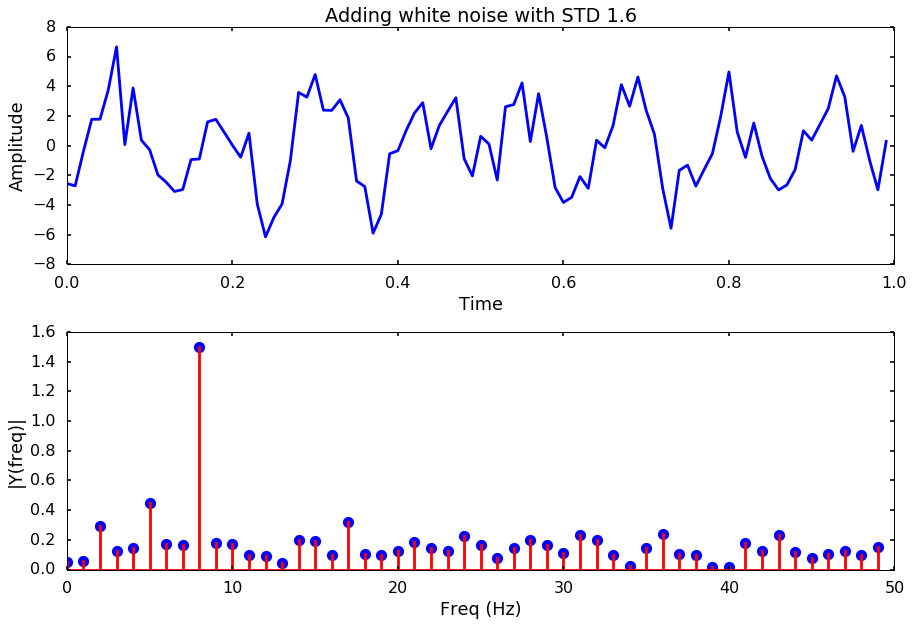
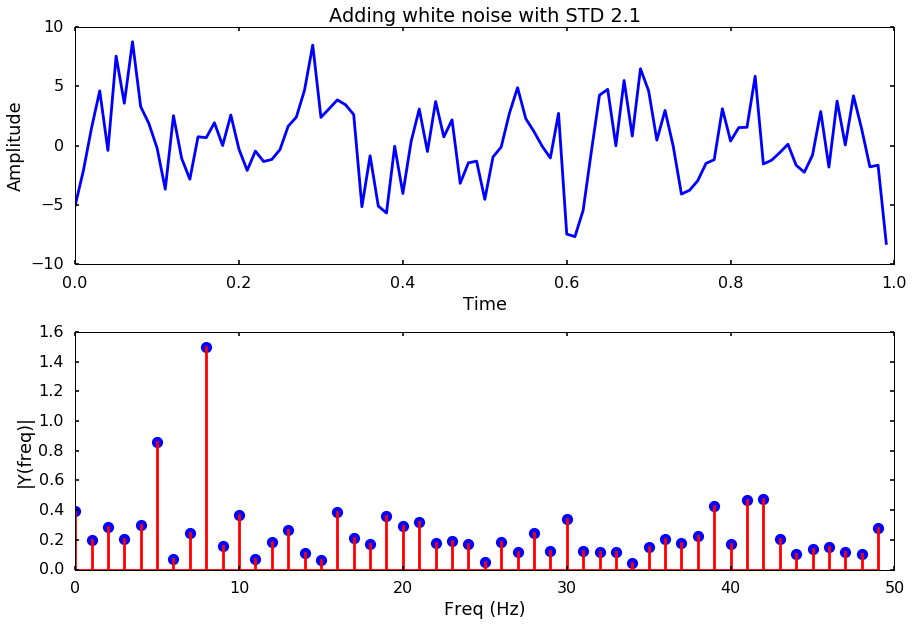
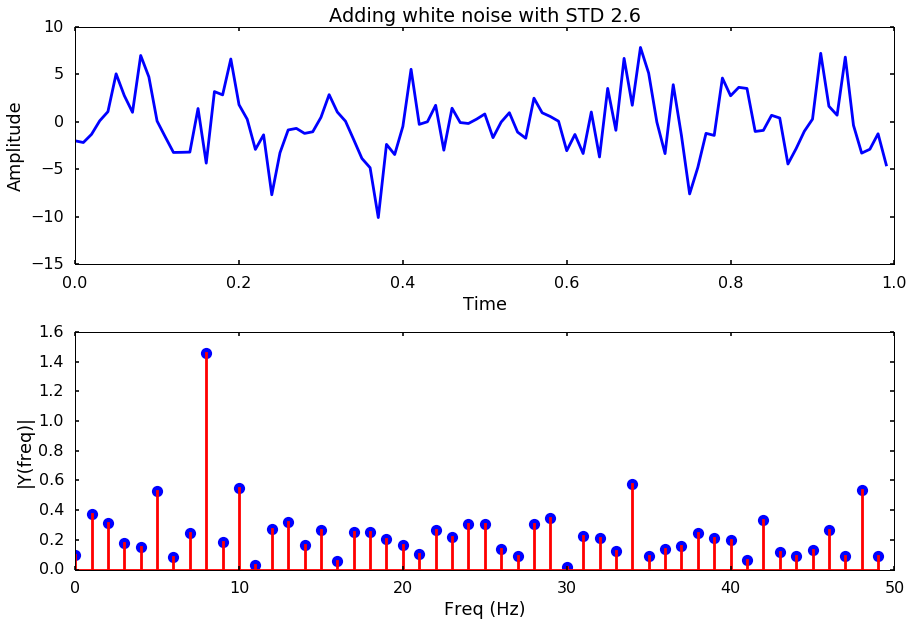
Next week, we will try to use different method to estimate the spectrum other than the simple FFT, and see if some method is better to get the frequency out even with a high-level of noise.
Hey there I am so delighted I found your website, I really found you by error, while I was looking on Yahoo for something else, Anyhow I am here now and would just like to say many thanks for a tremendous post and a all round interesting blog (I also love the theme/design), I don’t have time to read through it all at the moment but I have book-marked it and also included your RSS feeds, so when I have time I will be back to read much more, Please do keep up the fantastic job.
ReplyDeletedashiki print maxi skirt
Very well written post. Thanks for sharing this, I really appreciate you taking the time to share with everyone. Best pmp certification cost in india
ReplyDeleteFive weeks ago my boyfriend broke up with me. It all started when i went to summer camp i was trying to contact him but it was not going through. So when I came back from camp I saw him with a young lady kissing in his bed room, I was frustrated and it gave me a sleepless night. I thought he will come back to apologies but he didn't come for almost three week i was really hurt but i thank Dr.Azuka for all he did i met Dr.Azuka during my search at the internet i decided to contact him on his email dr.azukasolutionhome@gmail.com he brought my boyfriend back to me just within 48 hours i am really happy. What’s app contact : +44 7520 636249
ReplyDelete