Pause the update of the blog

I am currently working on writing a book, Python Programming and Numerical Methods: A Guide for Engineers and Scientists. This is a book will be used for the data science efforts at Berkeley Division of Data Sciences here and will be used as the textbook for a course next year. 

Therefore, I don't have time to update my blog before I can finish the book. My estimation to finish the book is about April 2019. Hopefully after that, I could continue to work on my blog. Thanks. 

Spell checking in Jupyter notebook markdown cells

These days, I started to write more and more in Jupyter notebook, not only my blog, but also an entire book within it. Therefore, spell checking is very important to me. But the online grammarly check doesn't work with the notebook, so that I need a new way to do it. 

After googling it, it seems adding the spell check for the markdown cell is easy. It is all based on the discussions here. The basic steps are:

pip install jupyter_contrib_nbextensions
jupyter contrib nbextension install --user
jupyter nbextension enable spellchecker/main

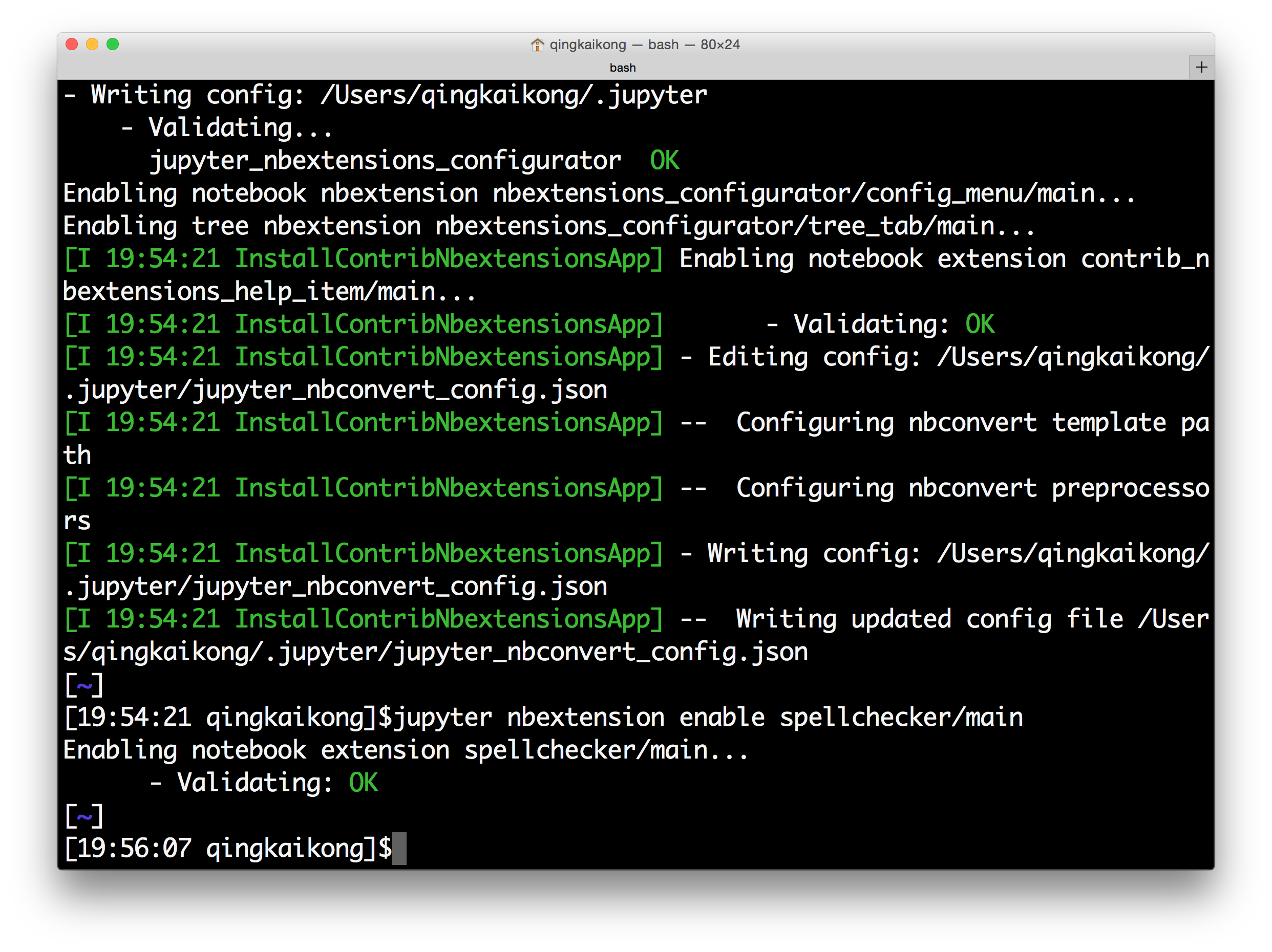
After successfully running the above commands, you should see the screen like this:

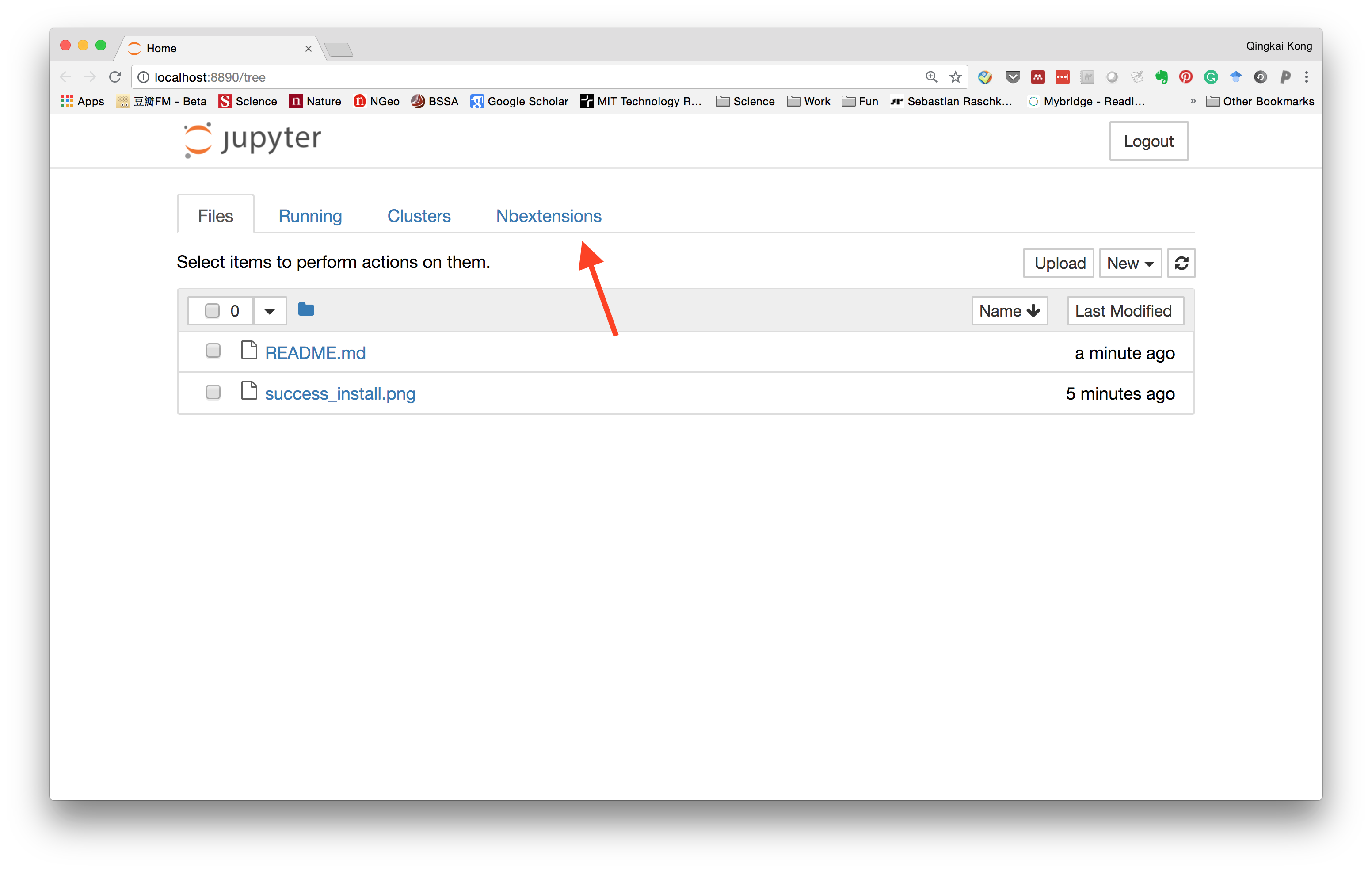
Now if you launch the Jupyter notebook, and in the dashboard, you will see a new option for the Nbextensions. 

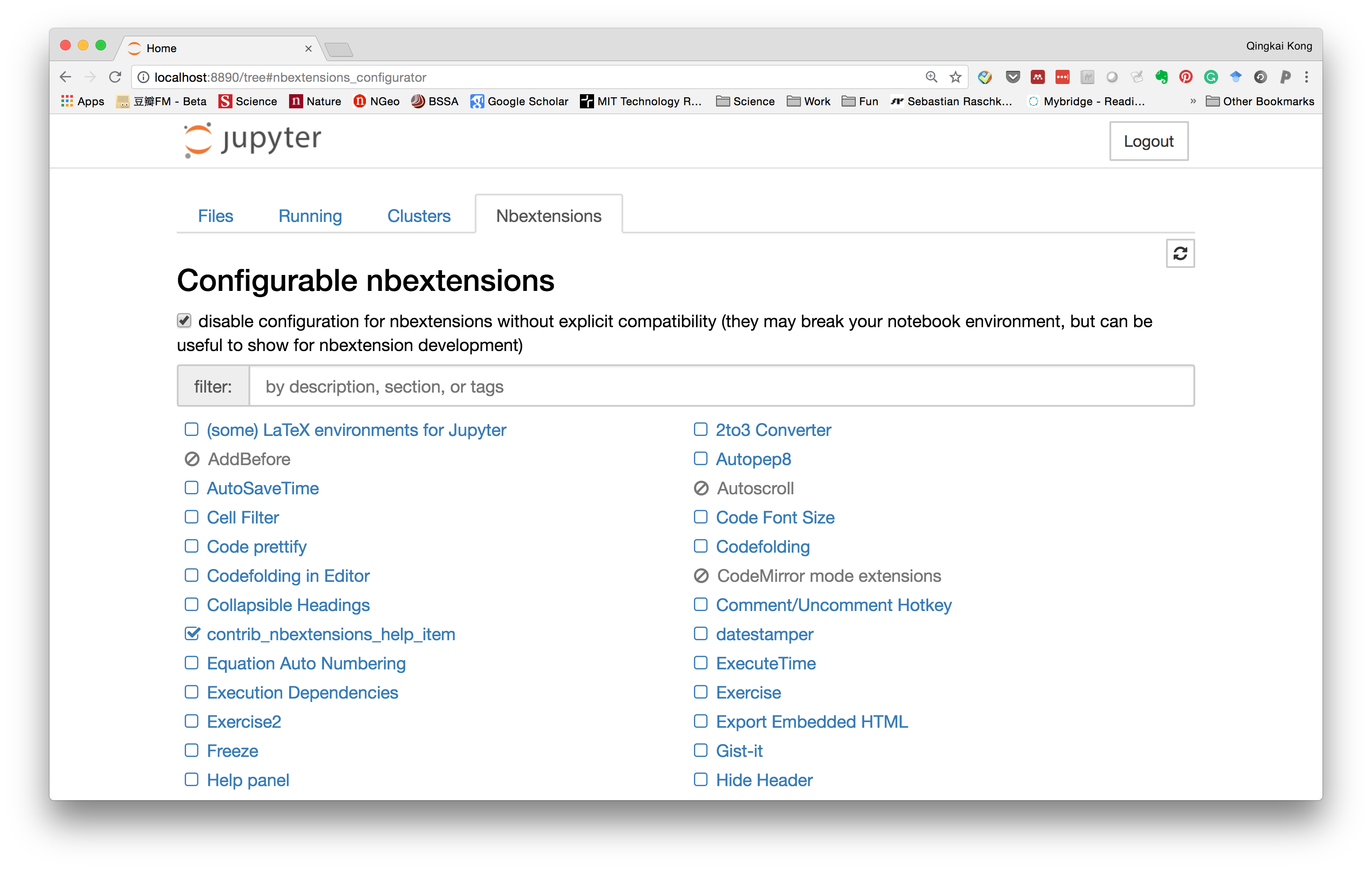
Within it, you can see all the extensions and the ones you enabled. 

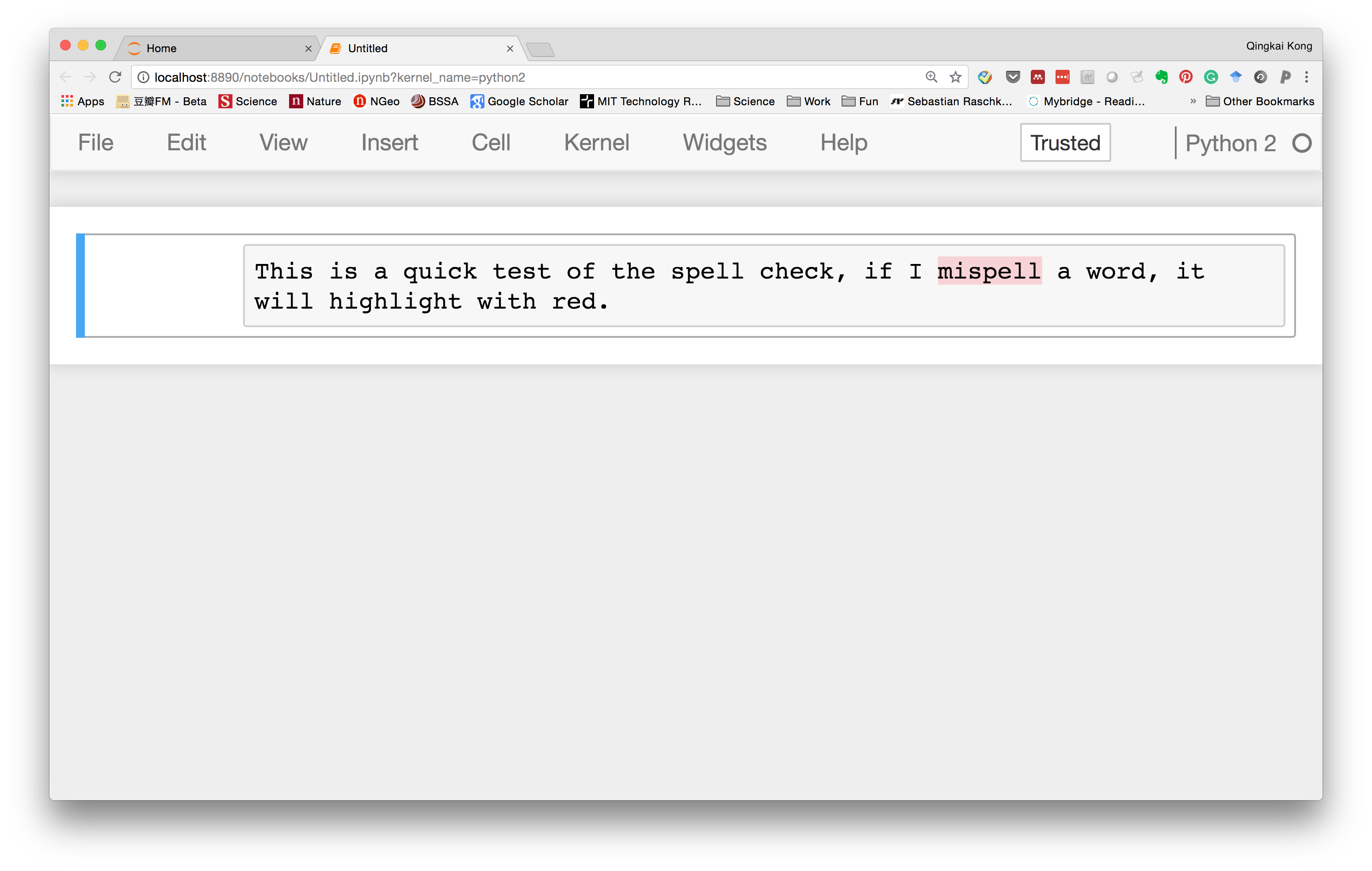
Now, let's go to the notebook, and type something in a markdown cell, we could see that it can highlight the word we misspelled. 

Quickly remove the old kernels for Jupyter

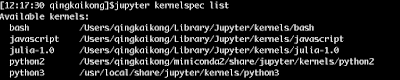
Over time, when we use Jupyter notebook or Jupyter lab, we will have more and more old kernels. As the following figure shows, I have the old Julia kernels that I want to get rid of.

Then I found it is very easy to get rid of these old kernels. The first thing we could do is to run the command to see what kernels do we have: jupyter kernelspec list

Then we could delete the old kernel by deleting the folder showing in the list and then install the new ones. See the following figure after I deleted the kernels and installed the new kernels. 

Slice datetime with milliseconds in Pandas dataframe

I use pandas a lot for dealing with time series. Especially the function that it could easily slice the time range you want. But recently, I need to slice between two timestamps with milliseconds, then it is not straightforward. It took me some time to figure it out (I didn't find any useful information online). Therefore, I just document it here if you have the same problem. You can find the notebook version of the blog on Qingkai's Github. 

import pandas as pd

First generate a dataframe with datetime as the index

Let's first generate a dataframe with datatime as the index and a counter as another column. 

## define the start and end of the time range
t0 = '2018-01-01 00:00:00.000'
t1 = '2018-01-02 00:00:00.000'

## generate the sequence with a step of 100 milliseconds
df_times = pd.date_range(t0, t1, freq = '100L', tz= "UTC")

## put this into a dataframe
df = pd.DataFrame()
df['datetime'] = df_times
df['count'] = range(len(df_times))
df = df.set_index('datetime')
df.head()

	count
datetime
2018-01-01 00:00:00+00:00	0
2018-01-01 00:00:00.100000+00:00	1
2018-01-01 00:00:00.200000+00:00	2
2018-01-01 00:00:00.300000+00:00	3
2018-01-01 00:00:00.400000+00:00	4

Let's slice a time range

We first slice the data between two times. We can see it works well without the milliseconds in the start and end time

df['2018-01-01 00:00:00':'2018-01-01 00:00:01']

	count
datetime
2018-01-01 00:00:00+00:00	0
2018-01-01 00:00:00.100000+00:00	1
2018-01-01 00:00:00.200000+00:00	2
2018-01-01 00:00:00.300000+00:00	3
2018-01-01 00:00:00.400000+00:00	4
2018-01-01 00:00:00.500000+00:00	5
2018-01-01 00:00:00.600000+00:00	6
2018-01-01 00:00:00.700000+00:00	7
2018-01-01 00:00:00.800000+00:00	8
2018-01-01 00:00:00.900000+00:00	9
2018-01-01 00:00:01+00:00	10
2018-01-01 00:00:01.100000+00:00	11
2018-01-01 00:00:01.200000+00:00	12
2018-01-01 00:00:01.300000+00:00	13
2018-01-01 00:00:01.400000+00:00	14
2018-01-01 00:00:01.500000+00:00	15
2018-01-01 00:00:01.600000+00:00	16
2018-01-01 00:00:01.700000+00:00	17
2018-01-01 00:00:01.800000+00:00	18
2018-01-01 00:00:01.900000+00:00	19

What if I want to slice two times with milliseconds as the following, we could see that we experience an error that has no information to help us to identify what happened. 

df['2018-01-01 00:00:00.500':'2018-01-01 00:00:01.200']

---------------------------------------------------------------------------

KeyError                                  Traceback (most recent call last)

~/miniconda2/envs/python3/lib/python3.6/site-packages/pandas/core/indexes/datetimes.py in slice_indexer(self, start, end, step, kind)
   1527         try:
-> 1528             return Index.slice_indexer(self, start, end, step, kind=kind)
   1529         except KeyError:


~/miniconda2/envs/python3/lib/python3.6/site-packages/pandas/core/indexes/base.py in slice_indexer(self, start, end, step, kind)
   3456         start_slice, end_slice = self.slice_locs(start, end, step=step,
-> 3457                                                  kind=kind)
   3458 


~/miniconda2/envs/python3/lib/python3.6/site-packages/pandas/core/indexes/base.py in slice_locs(self, start, end, step, kind)
   3657         if start is not None:
-> 3658             start_slice = self.get_slice_bound(start, 'left', kind)
   3659         if start_slice is None:


~/miniconda2/envs/python3/lib/python3.6/site-packages/pandas/core/indexes/base.py in get_slice_bound(self, label, side, kind)
   3583         # to datetime boundary according to its resolution.
-> 3584         label = self._maybe_cast_slice_bound(label, side, kind)
   3585 


~/miniconda2/envs/python3/lib/python3.6/site-packages/pandas/core/indexes/datetimes.py in _maybe_cast_slice_bound(self, label, side, kind)
   1480             _, parsed, reso = parse_time_string(label, freq)
-> 1481             lower, upper = self._parsed_string_to_bounds(reso, parsed)
   1482             # lower, upper form the half-open interval:


~/miniconda2/envs/python3/lib/python3.6/site-packages/pandas/core/indexes/datetimes.py in _parsed_string_to_bounds(self, reso, parsed)
   1317         else:
-> 1318             raise KeyError
   1319 


KeyError: 


During handling of the above exception, another exception occurred:


KeyError                                  Traceback (most recent call last)

<ipython-input-4-803941334466> in <module>()
----> 1 df['2018-01-01 00:00:00.500':'2018-01-01 00:00:01.200']


~/miniconda2/envs/python3/lib/python3.6/site-packages/pandas/core/frame.py in __getitem__(self, key)
   2125 
   2126         # see if we can slice the rows
-> 2127         indexer = convert_to_index_sliceable(self, key)
   2128         if indexer is not None:
   2129             return self._getitem_slice(indexer)


~/miniconda2/envs/python3/lib/python3.6/site-packages/pandas/core/indexing.py in convert_to_index_sliceable(obj, key)
   1978     idx = obj.index
   1979     if isinstance(key, slice):
-> 1980         return idx._convert_slice_indexer(key, kind='getitem')
   1981 
   1982     elif isinstance(key, compat.string_types):


~/miniconda2/envs/python3/lib/python3.6/site-packages/pandas/core/indexes/base.py in _convert_slice_indexer(self, key, kind)
   1462         else:
   1463             try:
-> 1464                 indexer = self.slice_indexer(start, stop, step, kind=kind)
   1465             except Exception:
   1466                 if is_index_slice:


~/miniconda2/envs/python3/lib/python3.6/site-packages/pandas/core/indexes/datetimes.py in slice_indexer(self, start, end, step, kind)
   1536                 if start is not None:
   1537                     start_casted = self._maybe_cast_slice_bound(
-> 1538                         start, 'left', kind)
   1539                     mask = start_casted <= self
   1540 


~/miniconda2/envs/python3/lib/python3.6/site-packages/pandas/core/indexes/datetimes.py in _maybe_cast_slice_bound(self, label, side, kind)
   1479                            getattr(self, 'inferred_freq', None))
   1480             _, parsed, reso = parse_time_string(label, freq)
-> 1481             lower, upper = self._parsed_string_to_bounds(reso, parsed)
   1482             # lower, upper form the half-open interval:
   1483             #   [parsed, parsed + 1 freq)


~/miniconda2/envs/python3/lib/python3.6/site-packages/pandas/core/indexes/datetimes.py in _parsed_string_to_bounds(self, reso, parsed)
   1316             return (Timestamp(st, tz=self.tz), Timestamp(st, tz=self.tz))
   1317         else:
-> 1318             raise KeyError
   1319 
   1320     def _partial_date_slice(self, reso, parsed, use_lhs=True, use_rhs=True):


KeyError: 

The solution

I found out an easy solution to the problem, instead of directly slice the data, we first find the index that meets our requirements, and then use the index to find the data as shown below:

ix = (df.index >= '2018-01-01 00:00:00.500') & (df.index <='2018-01-01 00:00:01.200')
df[ix]

My Researcher experience for one month

I've been in my new position - Assistant Data Science Researcher for one month now, it is so different than that of a Ph.D. student. I want to use this blog to document my experience with this new position for this one month.

First of all, I am a little surprised by this researcher position. Because at the beginning, I am a little sad that I didn't find a faculty position and think this researcher position is just an enhanced postdoc position. But after one month, I found this position is a light version of a faculty position that I could practice a lot of things I wouldn't have chance as a postdoc (actually, at some other university, this position is called - Research Professor, but at Berkeley, we don't have this title). Why light? (1) We don't have a startup as a faculty to start our research team; (2) We are on a soft-money position, which means that our salary has a certain percentage fixed, all the others that we need to write proposals to get myself funded (it ranges from 6 month - 12 months at different cases, luckily, I do have some portion come as fixed for now). In contrast, a faculty will have 9-month salary fixed, and only 3-month's salary needs to be raised every year, much better and easier than 6 to 12 month; (3) We can not grant degrees to students, at least for assistant researcher (I heard at a certain level, we could serve as the committee member of Ph.D. students, but I forgot when); (4) Researchers don't have the obligation to teach a class or serve administration services, all we need to do is to work on our research. I guess these are the main differences.

On the contrary, there are also many similarities between researcher and faculty position. (1) We could serve as a PI to apply for research grants; (2) We could build our own research team to work on interesting things; (3) We have similar ranks, i.e. assistant, associate, and full researchers.

Anyway, back to my experience of this one month. I was actively thinking about the following things as a researcher:

• Now I need to think more ideas and write proposals to get myself funded, and then potentially to start my research team by hiring some students/postdocs to work with me (of course, maybe co-advice with some faculties). 
• I think I should dream big at the beginning about set up this research team, this will determine my future level. Since if I could have a large research team by having some students working with me, then I could get more work done, which in turn may attract more funding. This is kind of like a positive feedback loop. 
• I should do something creative work, even though it may take longer time to get some publication, as long as it is something fun and could distinguish myself, I think it will worth pursuing. 
• I also found myself is deviated more and more from the technical work I really like to do, for example, programming, building machine learning models, etc. As a researcher, now I do more thinking, more meetings, more writing on proposals, but less technical work as I did as a student. But I guess this is good because I can really think something fun to work on, and then in the future to find some students to work out the ideas. 

Overall, it is a great experience, even though I do feel higher pressure now. But I am happy to practice and experience my skills on this light version of the faculty position. I hope in the near future, I could get a faculty position after improving my skills on this position. Let's see more things may change on me in the future......

My business card

I got my business card for my new position at Berkeley, I really like the design, see the following for my contact information. 

Setup Jupyter notebook for Julia

I think this week, the biggest news for me, maybe is Julia 1.0 released. It is a great language that I was thinking to learn for a long time (I just played it briefly before), therefore, I think I could use this 1.0 release as an excuse to learn it. 

Julia is a great language that has a goal to put the best features from different languages into one:

Using the reasons from Why we created Julia:

We want a language that’s open source, with a liberal license. We want the speed of C with the dynamism of Ruby. We want a language that’s homoiconic, with true macros like Lisp, but with obvious, familiar mathematical notation like Matlab. We want something as usable for general programming as Python, as easy for statistics as R, as natural for string processing as Perl, as powerful for linear algebra as Matlab, as good at gluing programs together as the shell. Something that is dirt simple to learn, yet keeps the most serious hackers happy. We want it interactive and we want it compiled.

See the key names of the languages: C, Ruby, Lisp, Matlab, Python, R, Perl, Shell, isn't really cool to learn this Julia! I will! 

Setup the environment

Let's see how could we setup the environment using Jupyter notebook + julia (I really like to work in Jupyter notebook, therefore, this is my first step to set it up). I assume you already had Jupyter notebook. 

1. Download Julia from - Download Julia
2. Add Julia into your .bashrc file - export PATH=/Applications/Julia-1.0.app/Contents/Resources/julia/bin:$PATH
3. In the terminal, open Julia
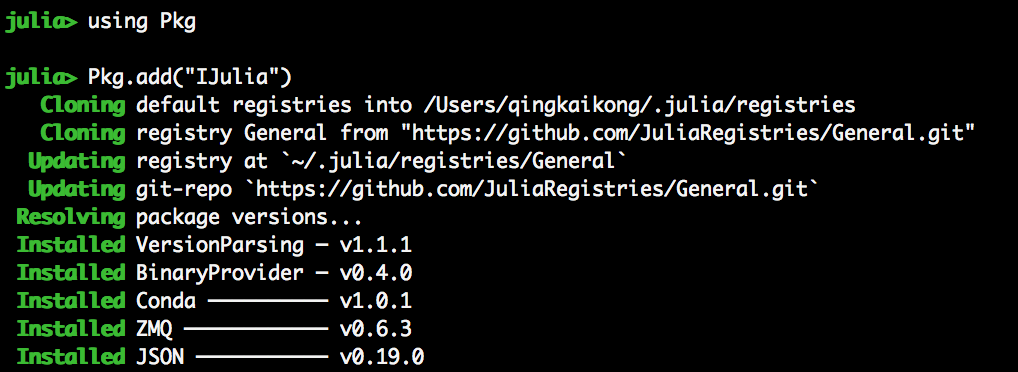
4. In Julia, install IJulia: 
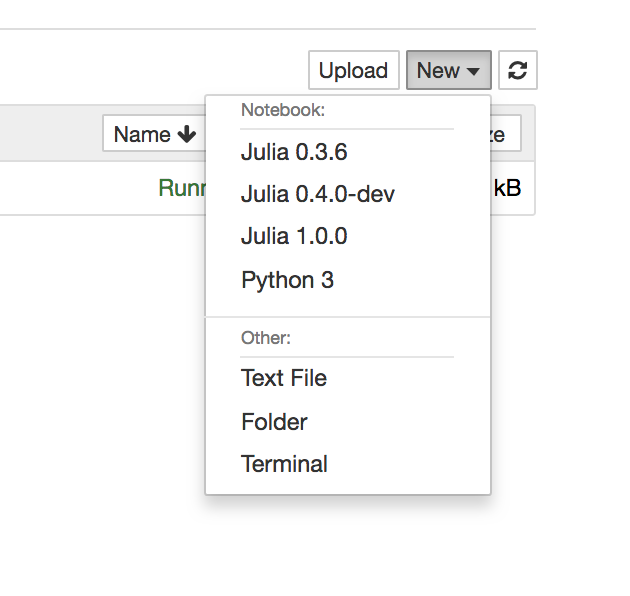
5. Open Jupter notebook, and select kernel: Julia 1.0.0 (note that, I had some old kernels when I played before) 
6. Let's run the famous 'Hello World!'

println("Hello World!")

Hello World!