The subspace detector is a method first designed to find repeating earthquakes, the basic idea is to form an orthonormal basis from a collection of representative waveforms that characterizing a particular repeating source. And then project the waveform data in some length window to this basis (or you can think of a weighted linear combination of the basis). Finally declare a detection by comparing the ratio of the energy in the projected data to the energy in the original data with a specific threshold.
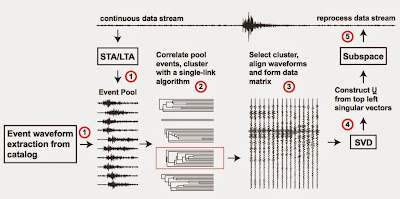
A quick step is here:
(1) Select a pool of events waveforms
(2) Calculate waveform correlations pairwise in the events pool and cluster them into groups based on the correlations.
(3) Select a cluster that related with the source characteristic you interest, align them and they call this as a design set, and calculated the orthonormal basis using SVD.
(4) Rank the singular vectors (basis) by the size of their corresponding singular value, so that they are actually sorted by the information they contained. And you can select to which order you want the basis to be, e.g. you think the first two or three vectors are sufficient to represent the original signal.
(5) Reprocess the data stream, project the data stream in a continuous window to the basis you selected, and then calculate the ratio of the projected data energy to the energy in the original data.
(6) Declare a detection when the ratio above certain threshold.
You can think of the ratio is some sort of correlation coefficient, since it ranges from 0 to 1 and resembles the square of a correlation coefficient.
The following figure is from the original paper (D. B. Harris 2006) which illustrate the procedure of the method:
The following figure is from the original paper (D. B. Harris 2006) which illustrate the procedure of the method:
