Machine learning 7 - Support Vector Machine - Part 1 - Intuitive SVMs

This week, let's have a look of the popular support vector machine (SVM). It can be used both in classification and regression problems. Like Artificial Neural Networks, SVM is also one of my favorite algorithms. It has a very different idea behind, and when you learn it, you will feel this algorithm tries to implement how we think. 

Let's start with a brief history of SVM. 

Brief history of SVM

1960 - Research started in 1960s.
1963-1964 - Study of the Margin. (Vapnik & Lerner and Vapnik and Chervonenkis)
1964 - Radial Basis Function (RBF) Kernels. (Aizerman)
1965 - Optimization formulation. (Mangasarian)
1971 - Kernels. (Kimeldorf and Wahba)
1992 - Modern SVMs from Boser, Guyon, and Vapnik (Vapnik et al)

We can see most of the research happens around 1960s - 1970s, and then SVM becomes famous when it gives comparable accuracy to the Artificial Neural Networks with elaborate features in handwriting recognition. 

In the next session, we will explore the idea behind the SVMs. After you get the basic idea, you will understand why it is called support vector machine. 

Intuitive Support Vector Machines

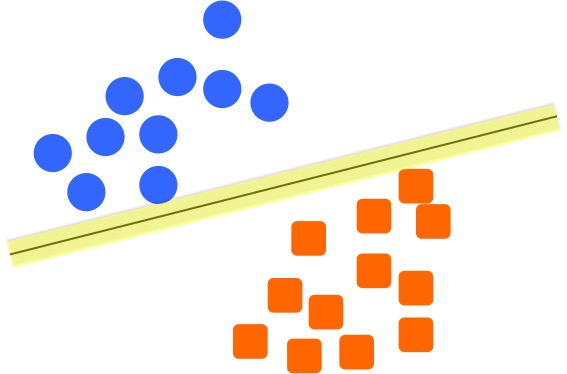
Let's say we have two classes like the following figure, blue circles and orange rectangles. Now we want to classify them, how can we do that? Well, we can simply draw a line between the two groups (see the red line), and separate them. If we have any new object to be classified, we can simply do this: if the new object falls above the line, we can say it belong to the blue circles. If it falls below the line, then it belongs to the orange group. 

But what if we draw another line, see the green line, it can also separate the two groups without any problems. 

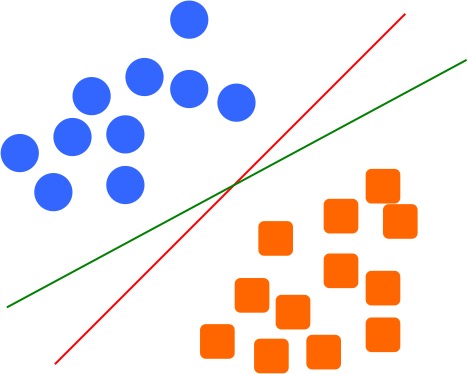
Same thing if we draw another blue line, the two groups can be classified using any of the 3 lines in the following figure. But the question is, which one we will choose as our model boundary to classify the two groups?

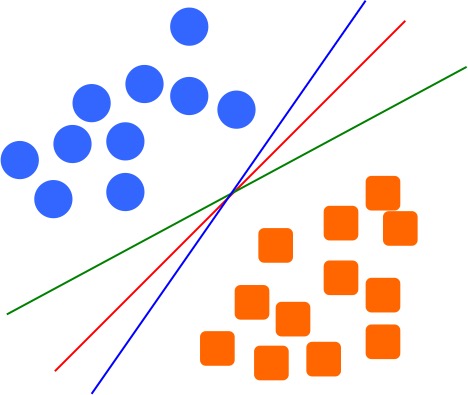
In fact, there can be infinite number of lines to separate the two groups, we need a way to select one to be our model. Which one you will choose? In a more extreme case, like the following figure, which line you want as your model, the red line, or the black line? 

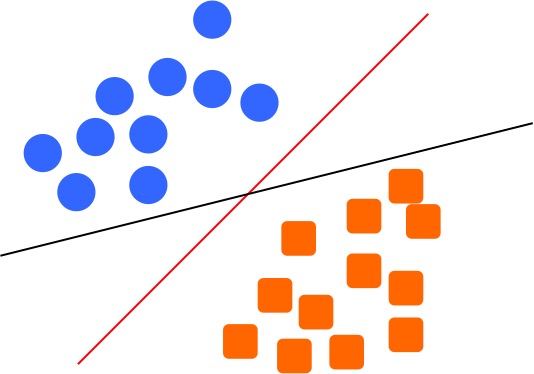
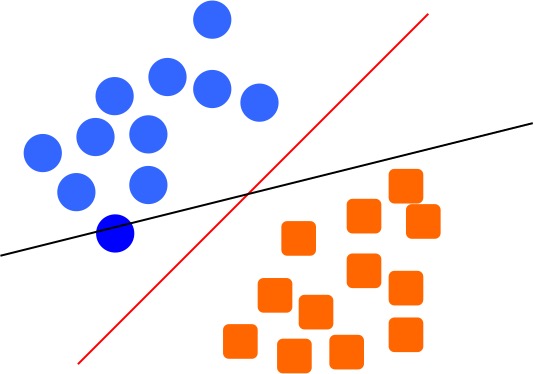
I guess most people will choose the red line as our boundary to separate the two groups. But why? What's the reason we choose the red line instead of the black line? You can say, it is just intuition: the black line is too close to the blue circle on the left, or too close to the red rectangle on the right. The red line seems far away from both groups, and it makes us feel safer to treat it as the boundary. Why feel safer? Because the further the boundary away from the groups, the less chance we will make mistakes if the object moves a little. For example, look at the following figure, if we have one blue circle (indicated as the darker blue) moves a little bit, it intersects with the black boundary. This is saying that, we might classify this blue circle as orange rectangle group, since it is fall on the other side of the boundary. But if we choose the red boundary, it will be correctly classified. This is why we say it feels safer to choose the red boundary, it will commit less errors. 

This intuition actually is the first motivation when researchers design the algorithm: we want to find a boundary that is far away from both groups. We can think the boundary line has a buffer zone shown as the yellow zone in the following figure, it can grow around the line until it touches circle and the rectangle at both sides. In the terminology in SVM, we can call this as margin. 

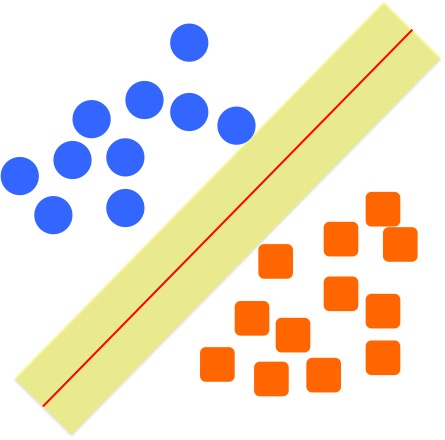
If we look at the margin of the black boundary, it will look like the following. Comparing with the margin of the red boundary, we can see this margin is much smaller in terms of size. 

Now, we have our rules to select the best boundary line: we want to select the boundary that has the largest margin - this is called maximize the margin in SVM. In order to find the largest margin, we can see that only some circles and the rectangles are useful to control the size of the margin. Let's look at the above two figures again, and we realize that, only the ones near the buffer zone seems useful. We can highlight them using a thick black outline, see the figure below, these are called support vectors, since they provide the support to control the margins. 

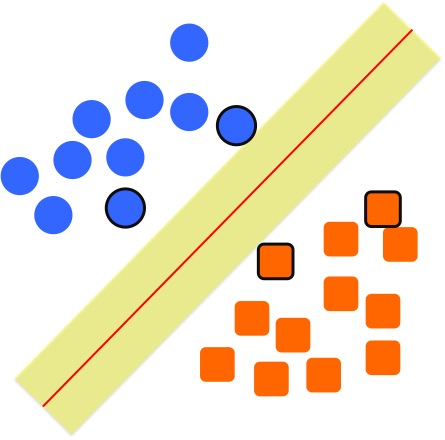
Now you can see where the name support vector machine comes from. Support vector relates what we talked above, and the machine is from the learning machines. 

Kernels

Support Vector Machine closely related with the kernels. We often hear people talking about kernel tricks in the SVM. But why do we need kernels, and what is kernels? As the goal of this blog is just to give you an intuitive concept, we will not talking too much details. 

In simple word, a kernel is just a transformation of our input data that allows the SVMs to process it more easily. For example, in the following case, we want to separate the blue and red circles. We can not just draw a linear line to separate them, but need a non-linear boundary, in this case, a circle boundary. 

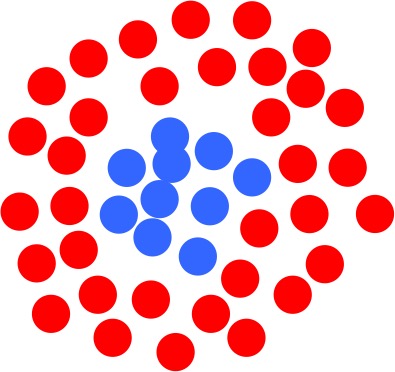
Instead of finding a circular boundary, kernel will help us to transform the input data into a higher dimension, and let us actually to use a linear boundary to separate the two groups. It will not be a linear line, but a linear plane. Let's look at the following movie to get a better sense how it works: 

              

I hope you have a good understanding of support vector machine now. And next week, let's try to use sklearn to classify some real problems. 

References

Support vector machine lecture from Caltech. It is a very nice lecture, where I first learned SVM from.
Introduction to statistical learning, a great free book that you can learn the basic machine learning. It has a chapter on SVM, which is really nice.