Explain of ICA
This week, let's talk about the Independent Component Analysis (ICA), which is a method that could separate the mixture of the signals back to the sources. Let's first see an example here:
The most famous example is the cocktail party effect: imagine a very simple case, that you are in a cocktail party that has 4 people, you, and A, B, C. You are talking with person A, and person B and C are in another conversation. Therefore, there are two conversations going on at the same time independently. Now, let's say, one conversation is signal 1 - s1 and the other one is signal 2 - s2. If we have two recorders near us at different place, they will record the two conversations that mixed together. Say r1 and r2 are the recorded conversations, they are from different mixing of the two signals s1, s2. As sounds can be summed linearly, therefore, r1 = a1 * s1 + b1 * s2, and r2 = a2 * s1 + b2 * s2. Now, from our recorded two signals, r1 and r2, is there a way we could find out the source s1 and s2?
This is where ICA comes in, it is a method that could help us to find the two signal sources from the mixed recordings. It is really useful, and belong to a larger area called blind signal separation. You can find all the code on Qingkai's Github.
Example below
Let's generate two signals and see if we could separate them. We use two different sources, one is a sine wave, and the other one is just a square wave.
import numpy as np
import matplotlib.pyplot as plt
plt.style.use('seaborn-poster')
%matplotlib inlinet = np.arange(0, 10, 0.1)
s1 = np.sin(2*t + 3)
s2 = np.sign(np.sin(3 * t))
Let's plot the two sources:
plt.figure(figsize = (10, 8))
plt.plot(t, s1, label = 'Source 1')
plt.plot(t, s2, label = 'Source 2')
plt.legend(loc = 2)
plt.xlabel('Time')
plt.ylabel('Amplitude')Text(0,0.5,'Amplitude')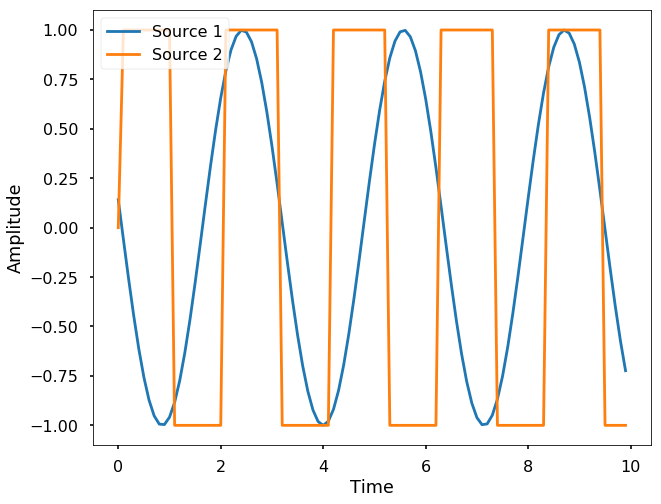
Now let's assume that we have two recorders that recorded the mixture of the two sources, but they emphasize the two sources differently (plus, we add in some white noise as well).
r1 = 2*s1 + 3*s2 + 0.05* np.random.normal(size=len(t))
r2 = 0.5*s1 + 2*s2 + 0.05 * np.random.normal(size=len(t))plt.figure(figsize = (10, 8))
plt.subplot(211)
plt.plot(t, r1, label = 'Recording 1')
plt.legend(loc = 2)
plt.xlabel('Time')
plt.ylabel('Amplitude')
plt.subplot(212)
plt.plot(t, r2, label = 'Recording 2')
plt.legend(loc = 2)
plt.xlabel('Time')
plt.ylabel('Amplitude')
plt.tight_layout()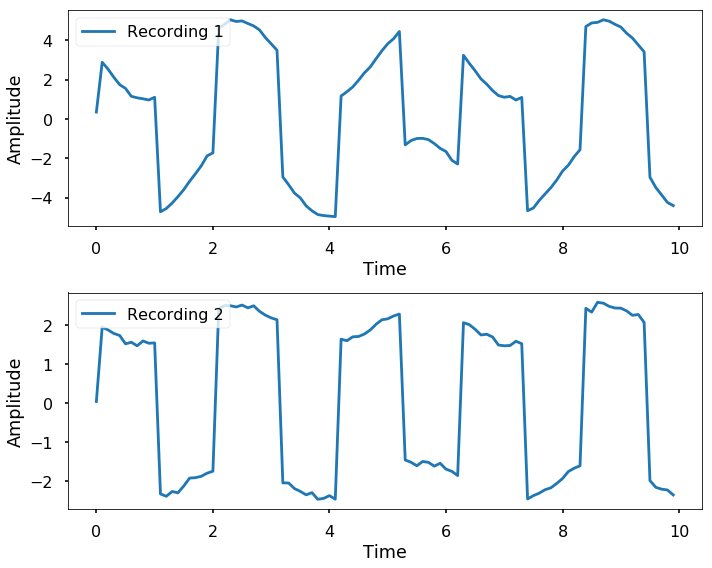
Now let's try to use ICA to separate the two signals.
from sklearn.decomposition import FastICAS = np.c_[r1, r2]
S /= S.std(axis=0) # Compute ICA
ica = FastICA(n_components = 2, random_state=2)
signal_ica = ica.fit_transform(S) # Reconstruct signals
A_ = ica.mixing_ # Get estimated mixing matrix
print(A_)[[4.41784919 8.97120998]
[1.98294353 9.80142515]]plt.figure(figsize = (10, 8))
l = plt.plot(signal_ica)
plt.legend(iter(l), ('Reconstructed source 1', 'Reconstructed source 2'), loc = 2)
plt.xlabel('Time')
plt.ylabel('Amplitude')Text(0,0.5,'Amplitude')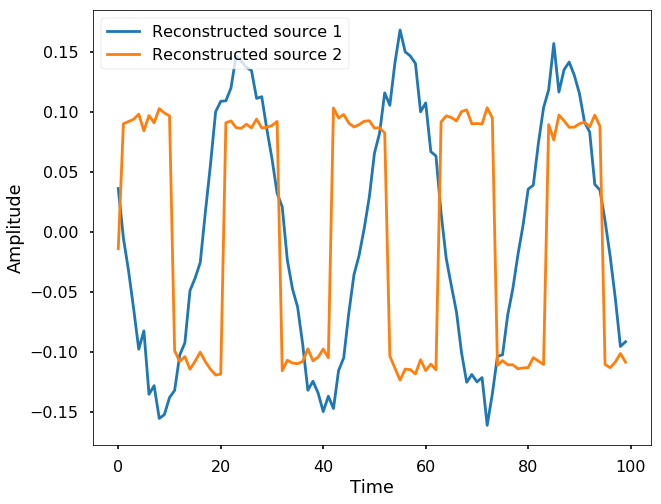
Am here to testify what this great spell caster done for me. i never believe in spell casting, until when i was was tempted to try it. i and my wife have been having a lot of problem living together, she will always not make me happy because she have fallen in love with another man outside our relationship, i tried my best to make sure that my wife leave this woman but the more i talk to her the more she makes me fell sad, so my marriage is now leading to divorce because she no longer gives me attention. so with all this pain and agony, i decided to contact this spell caster to see if things can work out between me and my wife again. this spell caster who was a man told me that my wife is really under a great spell that she have been charm by some magic, so he told me that he was going to make all things normal back. he did the spell on my wife and after 5 days my wife changed completely she even apologize with the way she treated me that she was not her self, i really thank this man his name is Dr ose he have bring back my wife back to me i want you all to contact him who are having any problem related to marriage issue and relationship problem he will solve it for you. his email is oseremenspelltemple@gmail.com he is a man and his great. wish you good time.
ReplyDeleteHe cast spells for different purposes like
(1) If you want your ex back.
(2) if you always have bad dream
(3) You want to be promoted in your office.
(4) You want women/men to run after you.
(5) If you want a child.
(6) You want to be rich.
(7) You want to tie your husband/wife to be yours forever.
(8) If you need financial assistance.
(9) HIV/AIDS CURE
(10) is the only answer to that your problem of winning the lottery
Contact him today on oseremenspelltemple@gmail.com or whatsapp him on +2348136482342
I was able to win back my Ex lover with the help of…. Dr.mac@yahoo.com..
DeleteFive weeks ago my boyfriend broke up with me. It all started when i went to summer camp i was trying to contact him but it was not going through. So when I came back from camp I saw him with a young lady kissing in his bed room, I was frustrated and it gave me a sleepless night. I thought he will come back to apologies but he didn't come for almost three week i was really hurt but i thank Dr.Azuka for all he did i met Dr.Azuka during my search at the internet i decided to contact him on his email dr.azukasolutionhome@gmail.com he brought my boyfriend back to me just within 48 hours i am really happy. What’s app contact : +44 7520 636249
ReplyDeleteThis comment has been removed by the author.
ReplyDeleteMy name is Tom cam!!! i am very grateful sharing this great testimonies with you all, The best thing that has ever happened in my life, is how i worn the Powerball lottery. I do believe that someday i will win the Powerball lottery. finally my dreams came through when i contacted Dr. OSE and tell him i needed the lottery winning special numbers cause i have come a long way spending money on ticket just to make sure i win. But i never knew that winning was so easy with the help of Dr. OSE, until the day i meant the spell caster testimony online, which a lot of people has talked about that he is very powerful and has great powers in casting lottery spell, so i decided to give it a try. I emailed Dr. OSE and he did a spell and gave me the winning lottery special numbers 62, and co-incidentally I have be playing this same number for the past 23years without any winning, But believe me when I play the special number 62 this time and the draws were out i was the mega winner because the special 62 matched all five white-ball numbers as well as the Powerball, in the April 4 drawing to win the $70 million jackpot prize...… Dr. OSE, truly you are the best, with Dr. OSE you can will millions of money through lottery. i am a living testimony and so very happy i meant him, and i will forever be grateful to him...… you can Email him for your own winning special lottery numbers now oseremenspelltemple@gmail.com OR WHATSAPP him +2348136482342
ReplyDeleteI've gotten back with my ex boyfriend with the help of Dr.jumba, the best spell caster online and I highly recommend Dr.jumba to anyone in need of help!.. I want to testify of how i got back my boyfriend after he breakup with me, we have been together for 3 years, recently i found out my boyfriend was having an affair with another Girl, when i confronted him, it led to quarrels and he finally broke up with me, i tried all i could to get him back but all to no avail until i saw a post in a relationship forum about a spell caster who helps people get back their lost love through Love spell, at first i doubted it but decided to give it a try, when i contacted this spell caster via his email, and he told me what to do and i did it, Then he did a Love spell for me. 28 hours later, my boyfriend really called me and told me that he misses me so much, So Amazing!! So that was how he came back that same day, with lots of love and joy, and he apologized for his mistake, and for the pain he caused me. Then from that day, our relationship was now stronger than how it were before, All thanks to DR.Jumba. he is so powerful and i decided to share my story on the Internet that Dr.Jumba real and powerful spell caster who i will always pray to live long to help his children in the time of trouble, if you are here and you need your Ex back or your husband moved to another woman, do not cry anymore, contact this powerful spell caster now. Here’s his contact: Email him at: wiccalovespelltools@gmail.com or wiccalovespelltools@yahoo.com, you can also call him or add him on WhatsApp: +19085174108 check out his website : drjumbaspellhome.wordpress.com
ReplyDeleteDR EMU WHO HELP PEOPLE IN ANY TYPE OF LOTTERY NUMBERS
ReplyDeleteIt is a very hard situation when playing the lottery and never won, or keep winning low fund not up to 100 bucks, i have been a victim of such a tough life, the biggest fund i have ever won was 100 bucks, and i have been playing lottery for almost 12 years now, things suddenly change the moment i came across a secret online, a testimony of a spell caster called DR EMU, who help people in any type of lottery numbers, i was not easily convinced, but i decided to give try, now i am a proud lottery winner with the help of DR EMU, i won $1,000.0000.00 and i am making this known to every one out there who have been trying all day to win the lottery, believe me this is the only way to win the lottery.
Contact him via email Emutemple@gmail.com
What's app +2347012841542
Https://emutemple.wordpress.com/
I'm Melvin Martins. from the United States. I started playing lottery games 7 years ago and I have never won big. I went online to seek help on how I can win big in my lottery games and I saw some nice reviews about Dr John who has made different people huge winners in their lottery games with his prayers. I gave it a try and I contacted Dr John who told me how and what to do before I can become a big lotto winner and I accepted. He made special prayers for me at his temple and gave me the required numbers to play the lotto game and when I played it, I won a massive $235.4 million POWERBALL jackpot. I was so happy and I chose to receive my winnings in a one-time, lump-sum payment of $160,038,447.27 at Florida Lottery Headquarters in Tallahassee and the balance was given to the store that I bought & played the game from. I would love other people to seek help from him and he can be contacted through WhatsApp/call/text via this number +1 (803) 820 2671 or you can email him on: Drjohnwinlotterspell@gmail.com .
ReplyDeleteGood day everybody, This is my testimony on how i won $4,200,201 million I want to use this opportunity to thank Great JOHN for helping me to win the lottery of $4,200,201 million dollars on Mega millions lottery ticket. I have been playing the lottery for the past 6 years now and I have never won. Ever since then I have not been able to win and I was so upset and I needed help to win the lottery. So I decided to go online and search for help, there i saw so many good testimonies about this man called Great JOHN of how he has cast lucky spell lotto for people to win the lottery. I contacted him also and told him I want to win a lottery, he cast a spell for me which I use and I played and won $4,200,201 million dollars. I am so grateful to this man, just in-case you also need him to help you win, you can contact him through his email: Drjohnwinlotterspell@gmail.com, WhatsApp number: +1 (803) 820 2671 ..
ReplyDeleteMany people have written articles about how they were helped but I am very grateful to this great man who brought my ex-husband back to me. This testimony is a true story and my name is Jennifer Sanchez. When I came in contact with this man was also through a testimony written about him helping with a cure for Herpes Virus and I have also encountered many testimonies about how he has been helping others with their life. To get back with an ex is one of the most innermost feelings many people would love to experience especially as those memories with our ex always cloud our mind when someone else does some of those things our ex used to do. I was a single parent of two boys for almost 6 years and though my ex-husband was not staying with me and the kids I still wish someday he will return to me. This doctor I encountered is known as Dr. Odunga helped me with my wishes and I am happy to write on this website that my ex-husband is back with me. I am very happy to share the testimony with everyone so that they too can meet this great doctor and solve their problems. I don't know what others might feel about getting their ex back in their life but I always know there is a blessing in disguise with just a single re-connection with an ex. If you want to successfully get back with your ex or facing an infertility problem, contact this great man at odungaspelltemple@gmail.com Or WhatsApp/Call +2348167159012 and share an awesome testimony too just as I did
ReplyDelete
ReplyDeleteHi everyone my name is Anna Eriksen i want to share my amazing testimony on how Dr Ayoba blessed my life, i am a sale girl in supper market, i have been playing lottery game for long now and i don’t usually win, i came across a testimony of someone testifying about how Dr Ayoba prayed for him and gave him a lottery game to play and he won big amount of money, so i also decided to try my luck, i contact him through his WhatsApp number and he assured me that he will help me, he told me it will take him 24 hours to pray for me, so on the after the 24 hours he gave me some lottery numbers to play and i went to play the game so on that faithful day i went to check the game to my greatest surprise i won a very big amount $434.2 million that changed my life and my status, i quit working as a sale girl in the supper market and i became a business owner. I want you out there to also contact him for your lucky game. You can reach him via his Email drayobasolutionhome@gmail.com or WhatsApp him on +1 (708) 736‑1766
Thanks for the post! if you are struggling with your assignment work and want expert help then visit assignment help australia
ReplyDelete