This week, we will briefly talk about kernel density estimation, which is a useful way to estimate the probability density function of a random variable. The idea is quite simple, let's start by showing you example of density estimation using a Gaussian kernel for 1D case. You can find all the code at Qingkai's Github.
import numpy as np
import matplotlib.pyplot as plt
plt.style.use('seaborn-poster')
%matplotlib inlineGenerate a random 1D dataset
We first generate a bi-modal distribution using two Gaussians.
np.random.seed(12)
X = np.concatenate((np.random.normal(loc = -5, scale= 2, size = 100), np.random.normal(loc = 10, scale= 3, size = 100)))
# let's shuffle the order of the data (this is most for the animation later)
np.random.shuffle(X)
plt.figure(figsize = (10,8))
plt.hist(X, bins = 15, normed=True)
plt.plot(X, np.zeros(len(X)), '*k')
plt.ylim((-0.01, 0.1))
plt.xlabel('Values')
plt.ylabel('Frequencies')
plt.show()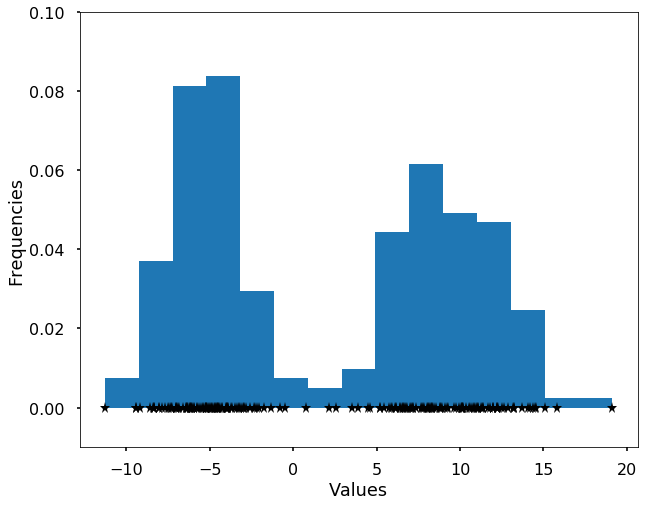
Define gaussian kernels
We define the Gaussian kernels as the following function, and we generate a grid and plot an example of Gaussian kernel centered at 5.
def gaussian_kernel(x, mu, sigma):
return 1/(sigma * np.sqrt(2 * np.pi)) * np.exp( - (x - mu)**2 / (2 * sigma**2) )
# generate grid
min_v = np.min(X)
max_v = np.max(X)
grid = np.linspace(min_v, max_v, 100)
# plot out the example
plt.figure(figsize = (10,8))
plt.plot(grid, gaussian_kernel(grid, mu = 5, sigma = 1.0))
plt.title('Example of a kernel centered at 5')
plt.show()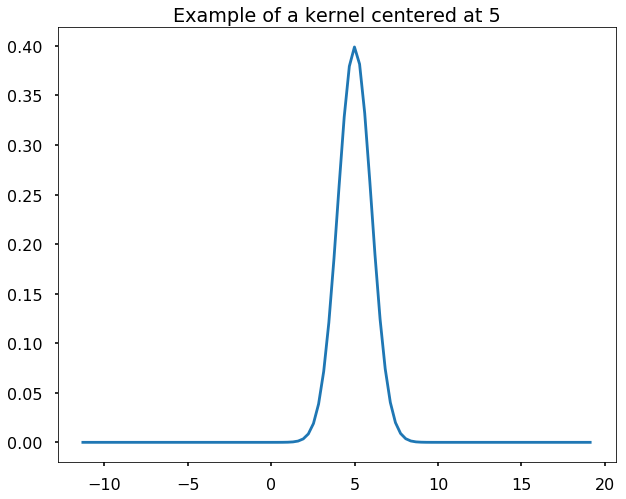
Estimate the density using the kernels
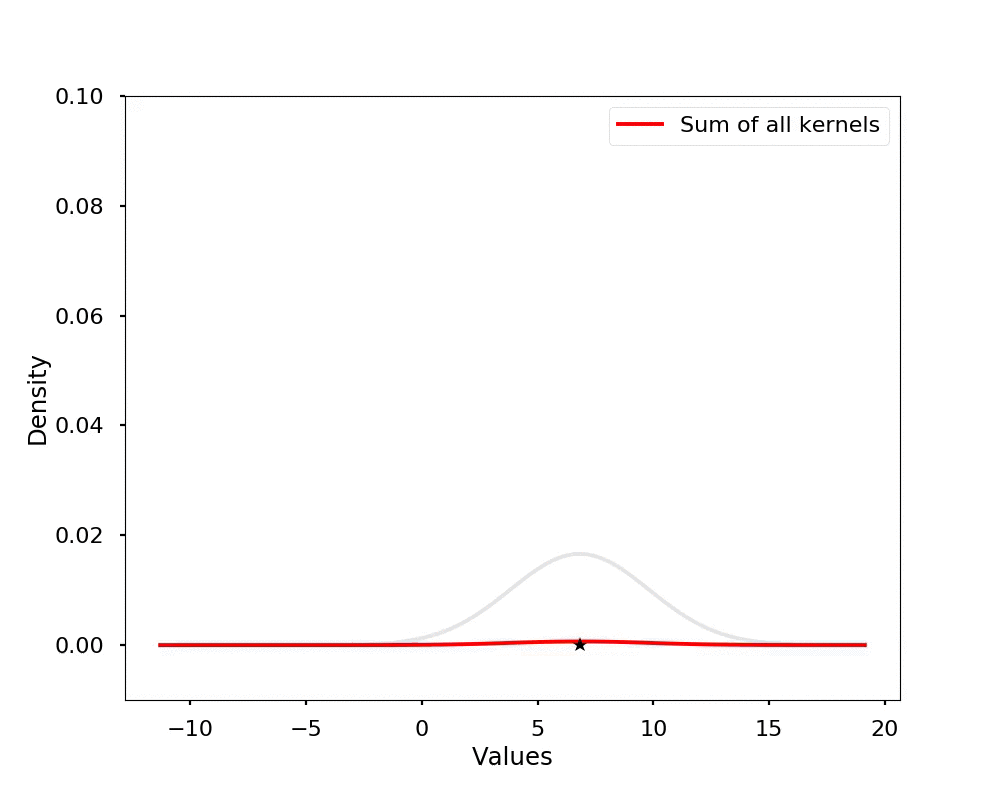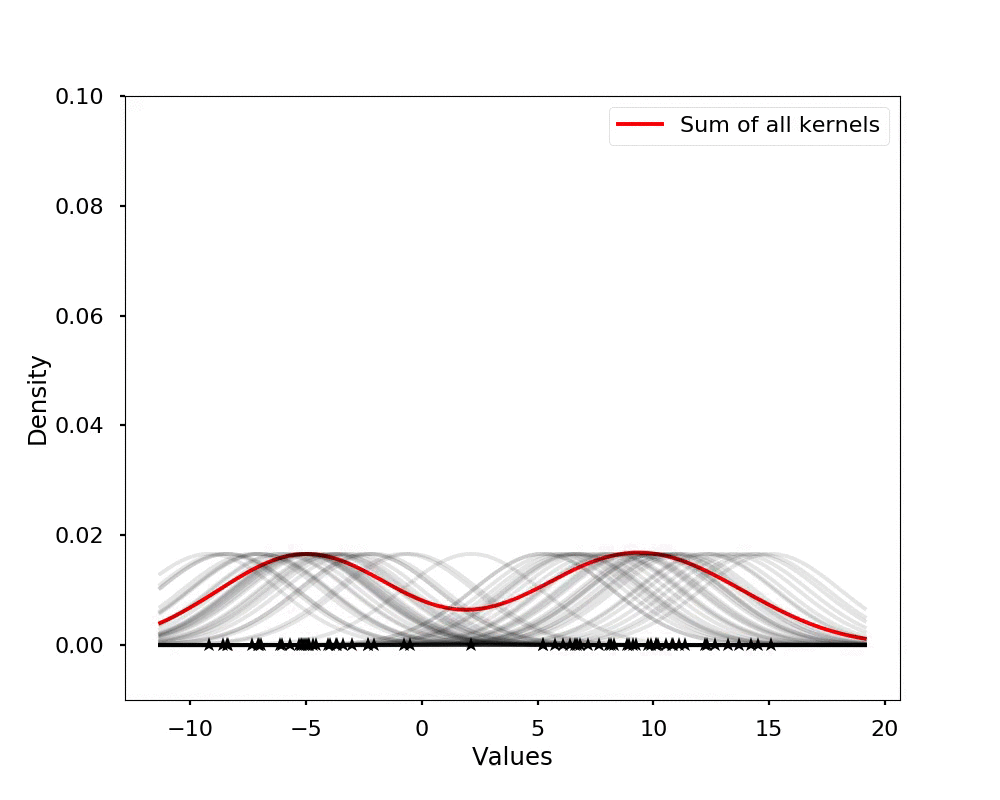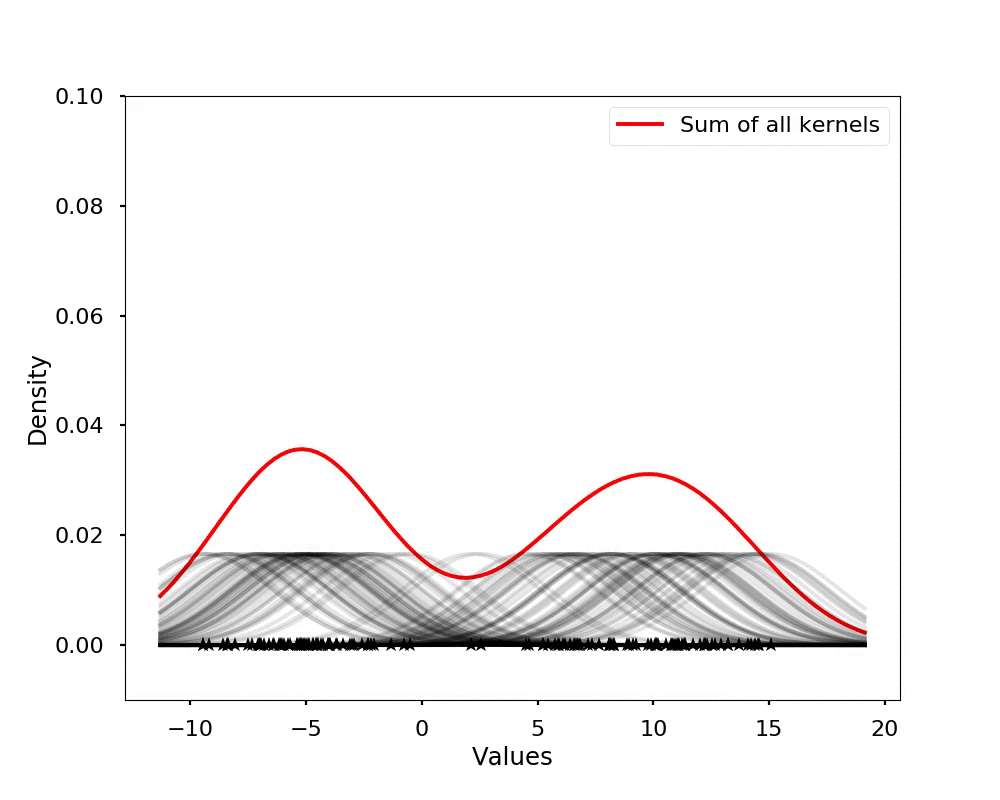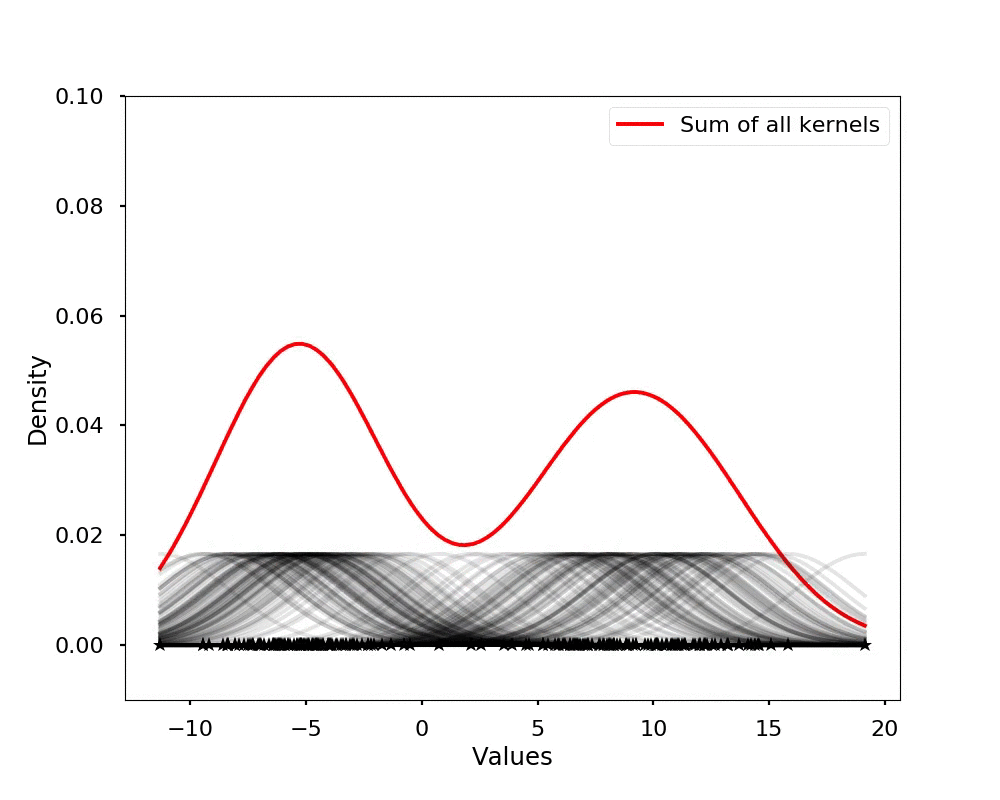
The kernel density estimation is actually very simple, you can think that for each data point, we will center a Gaussian kernel at it, and then we just sum all the kernels, we will have the kernel density estimation. The following is an animation that shows this process, we add one kernel at a time (the grey curves), the red curve is our density estimation that sums up all the grey curves. Note that, the width of the kernel has an effect of the smoothness of the density estimation, see the following example.
density_estimation = np.zeros(len(grid))
FFMpegWriter = manimation.writers['ffmpeg']
metadata = dict(title='Kernel density estimation', artist='Qingkai Kong',
comment='This is for gaussian kernels')
writer = FFMpegWriter(fps=10, metadata=metadata)
fig = plt.figure(figsize = (10,8))
line1, = plt.plot(grid, density_estimation, 'r-', label = 'Sum of all kernels')
plt.ylim(-0.01, 0.1)
plt.legend()
plt.xlabel('Values')
plt.ylabel('Density')
with writer.saving(fig, "Kernel_density_estimation.mp4", 100):
for x in X:
plt.plot(x, 0, '*k')
kernel = gaussian_kernel(grid, mu = x, sigma = 1.0)
density_estimation += kernel / len(X)
plt.plot(grid, kernel / 8, 'k', alpha = 0.1)
line1.set_data(grid, density_estimation)
writer.grab_frame()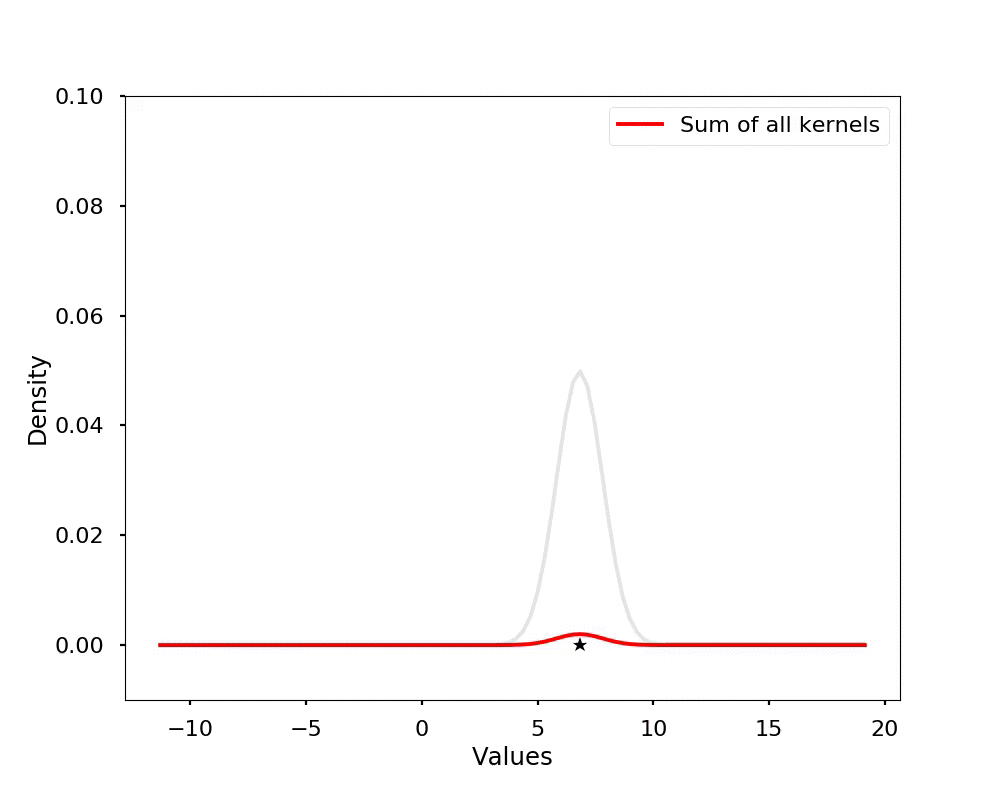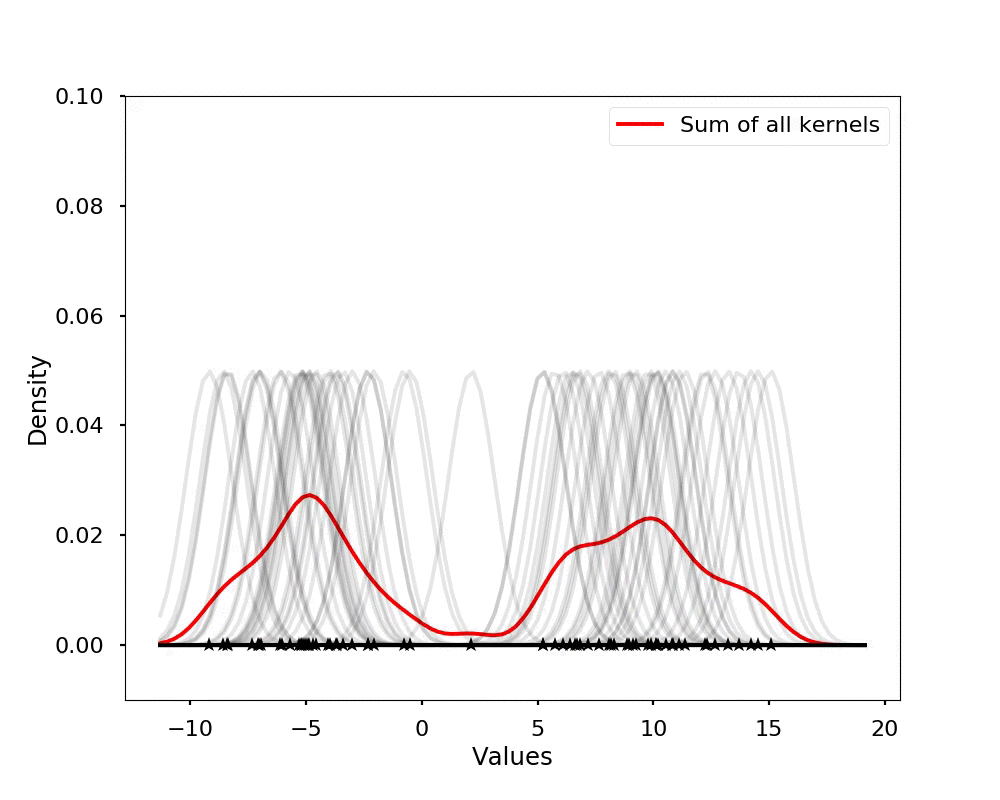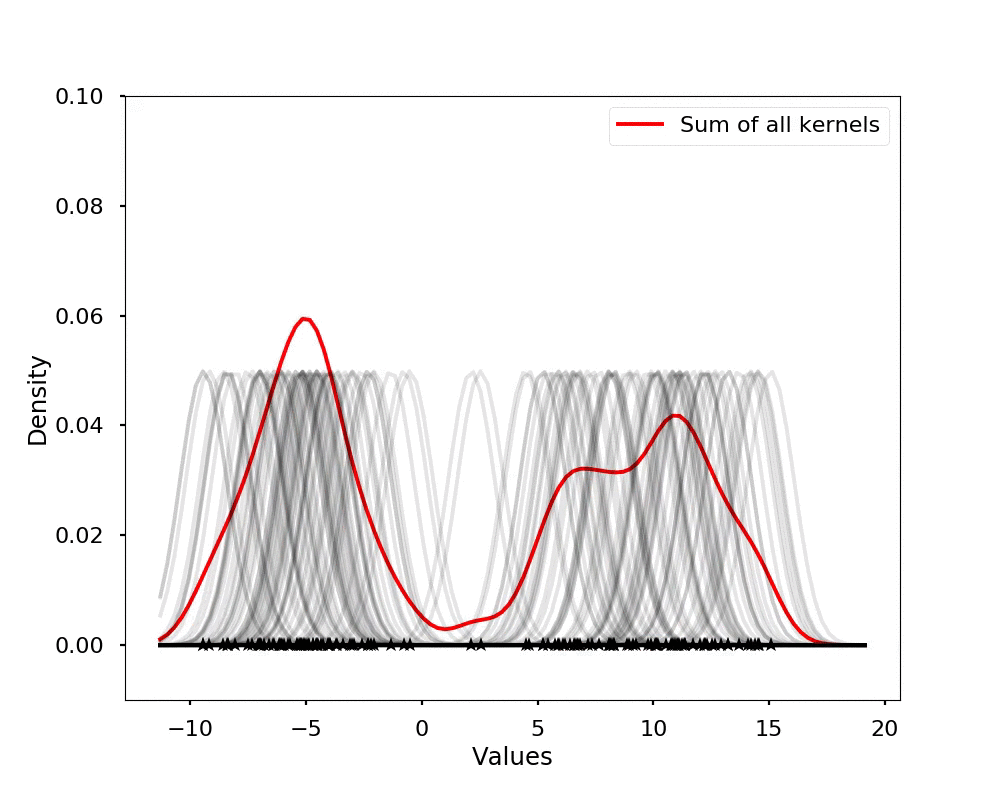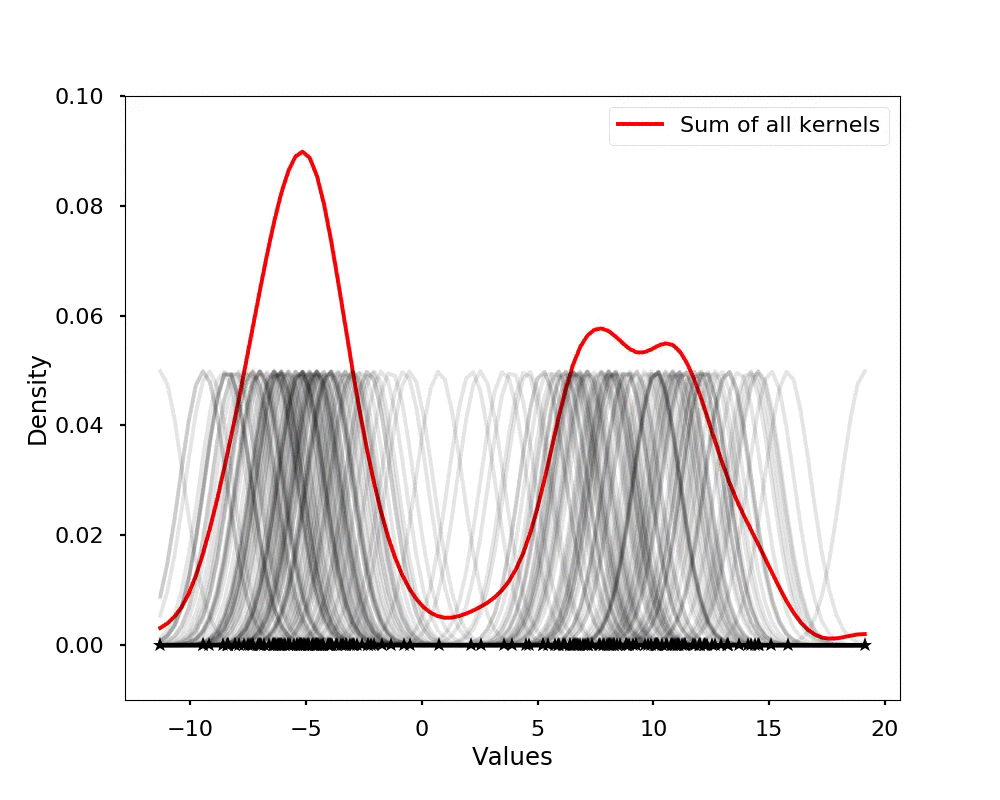
Let's see the effect on the density estimation using a wider kernel.
Kernel density estimation using Scipy
The above code is just to show you the basic idea of the kernel density estimation. In reality, we don't need to write the code by ourselves, we could use the existing packages, either scipy or sklearn. Here we show the example using scipy. We could see that the derived density estimation is very similar to what we got above.
from scipy import statskernel = stats.gaussian_kde(X, 0.1)
plt.figure(figsize = (10,8))
plt.plot(grid,kernel.evaluate(grid), 'r-')
plt.xlabel('Values')
plt.ylabel('Density')
plt.show()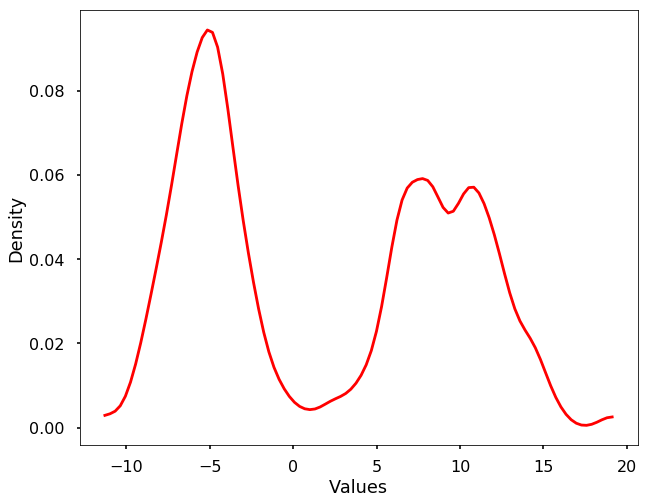
2D density estimation
Besides, we could expand this density estimation into 2 dimensions. The idea is still the same, instead of using the 1D Gaussian kernel to add up to the density estimation, now we use the 2D Gaussian kernels to do the estimation. Let's see the example using scipy for this 2D case.
# generate data
np.random.seed(12)
X = np.concatenate((np.random.normal(loc = -5, scale= 2, size = (100,2)), np.random.normal(loc = 10, scale= 3, size = (100,2))))
# get the mesh
m1, m2 = X[:, 0], X[:, 1]
xmin = m1.min()
xmax = m1.max()
ymin = m2.min()
ymax = m2.max()
# get the density estimation
X, Y = np.mgrid[xmin:xmax:100j, ymin:ymax:100j]
positions = np.vstack([X.ravel(), Y.ravel()])
values = np.vstack([m1, m2])
kernel = stats.gaussian_kde(values)
Z = np.reshape(kernel(positions).T, X.shape)
# plot the result
fig, ax = plt.subplots(figsize = (10,8))
plt.imshow(np.rot90(Z), cmap=plt.cm.jet,
extent=[xmin, xmax, ymin, ymax])
plt.colorbar()
ax.plot(m1, m2, 'k.', markersize=5)
ax.set_xlim([xmin, xmax])
ax.set_ylim([ymin, ymax])
plt.xlabel('X values')
plt.ylabel('y values')
plt.show()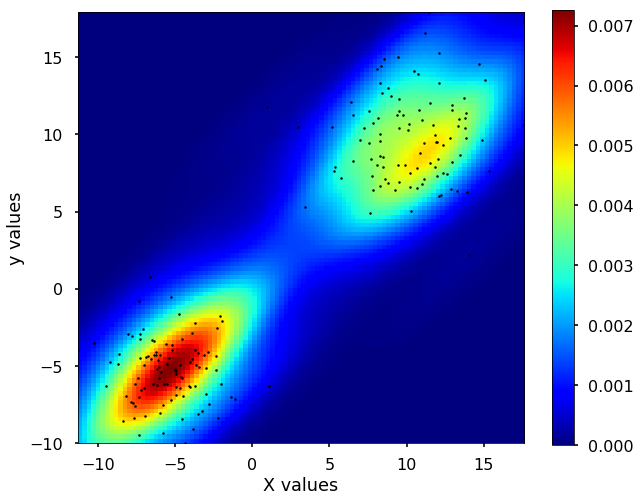
An equipment glitch brought down the gift page usefulness, back-end announcing apparatuses, and the sparkling new constant pioneer sheets and information representation, across the board singular motion.friv Games online 2020
ReplyDeleteJogos live
friv game
Five weeks ago my boyfriend broke up with me. It all started when i went to summer camp i was trying to contact him but it was not going through. So when I came back from camp I saw him with a young lady kissing in his bed room, I was frustrated and it gave me a sleepless night. I thought he will come back to apologies but he didn't come for almost three week i was really hurt but i thank Dr.Azuka for all he did i met Dr.Azuka during my search at the internet i decided to contact him on his email dr.azukasolutionhome@gmail.com he brought my boyfriend back to me just within 48 hours i am really happy. What’s app contact : +44 7520 636249
DeleteAm here to testify what this great spell caster done for me. i never believe in spell casting, until when i was was tempted to try it. i and my wife have been having a lot of problem living together, she will always not make me happy because she have fallen in love with another man outside our relationship, i tried my best to make sure that my wife leave this woman but the more i talk to her the more she makes me fell sad, so my marriage is now leading to divorce because she no longer gives me attention. so with all this pain and agony, i decided to contact this spell caster to see if things can work out between me and my wife again. this spell caster who was a man told me that my wife is really under a great spell that she have been charm by some magic, so he told me that he was going to make all things normal back. he did the spell on my wife and after 5 days my wife changed completely she even apologize with the way she treated me that she was not her self, i really thank this man his name is Dr ose he have bring back my wife back to me i want you all to contact him who are having any problem related to marriage issue and relationship problem he will solve it for you. his email is oseremenspelltemple@gmail.com he is a man and his great. wish you good time.
ReplyDeleteHe cast spells for different purposes like
(1) If you want your ex back.
(2) if you always have bad dream
(3) You want to be promoted in your office.
(4) You want women/men to run after you.
(5) If you want a child.
(6) You want to be rich.
(7) You want to tie your husband/wife to be yours forever.
(8) If you need financial assistance.
(9) HIV/AIDS CURE
(10) is the only answer to that your problem of winning the lottery
Contact him today on oseremenspelltemple@gmail.com or whatsapp him on +2348136482342
My name is Tom cam!!! i am very grateful sharing this great testimonies with you all, The best thing that has ever happened in my life, is how i worn the Powerball lottery. I do believe that someday i will win the Powerball lottery. finally my dreams came through when i contacted Dr. OSE and tell him i needed the lottery winning special numbers cause i have come a long way spending money on ticket just to make sure i win. But i never knew that winning was so easy with the help of Dr. OSE, until the day i meant the spell caster testimony online, which a lot of people has talked about that he is very powerful and has great powers in casting lottery spell, so i decided to give it a try. I emailed Dr. OSE and he did a spell and gave me the winning lottery special numbers 62, and co-incidentally I have be playing this same number for the past 23years without any winning, But believe me when I play the special number 62 this time and the draws were out i was the mega winner because the special 62 matched all five white-ball numbers as well as the Powerball, in the April 4 drawing to win the $70 million jackpot prize...… Dr. OSE, truly you are the best, with Dr. OSE you can will millions of money through lottery. i am a living testimony and so very happy i meant him, and i will forever be grateful to him...… you can Email him for your own winning special lottery numbers now oseremenspelltemple@gmail.com OR WHATSAPP him +2348136482342
ReplyDeleteI never thought I would be known for winning the lottery in NEW YORK. I am so grateful to DR AMBER for all he has done for me. I wouldn't have been able to win a CENT on the lottery if not for the help of DR AMBER who gave me perfect winning numbers to play the lottery that made me the winner of $10,000,000 DOLLARS in 2019. I got in touch with him again on his webpage: [ https://amberlottotemple.com ] in request for sure winning numbers to play the lottery. He told me what to do and I did all he instructed & required to get the spell prepared for me and within 3 days, he gave me the perfect numbers to play the lottery and could you believe that I won $10,000,000 DOLLARS after playing the lottery making it the second time I have won and I haven't finished spending the last one I won in 2019. DR AMBER is truly a God sent and I highly recommend him to anyone that needs help to win the lottery. You can message him on WhatsApp with +1 318-306-5044 or email: amberlottotemple@yahoo.com
ReplyDeleteJUAN HERNANDEZ FROM NEW YORK, USA.
I am a 59-year-old IT worker and it was going to be our 25-year wedding anniversary but we had no money to celebrate it. I was given an assignment in the office so I went online to search for answers when I saw testimonies of people thanking lord Bubuza for giving them the right lottery winning numbers, so I contacted lord Bubuza via WhatsApp: +1 951 442 2214. He gave me the lottery winning number after casting a spell and i won $1,000,000. My name is Licette Griffinm. Contact him via WhatsApp:+1 951 442 2214 or call: +1 507 400 0072 or email: lordbubuzamiraclework @ hotmail . com
ReplyDeleteI’ve heard plenty about spells but have never attempted it and the one time I did, it was successful for me. LORD MEDUZA performed a spell for me and provided the winning number that allowed my husband and I to win the Lotto. I returned home from the hospital where my baby was born and asked my husband to buy a Lotto Max ticket after seeing on social media that the Jackpot was at $70 million, mentioning that I’d found someone who could assist us in winning it and we proceeded exactly as LORD MEDUZA directed with the ticket. The next morning, I used my phone to check the ticket and heard a winning tone. I was in disbelief and unable to comprehend what was occurring, I looked at the ticket once more and I saw the same thing. That’s when I phoned my husband to tell him we had won. Thus, anyone seeking assistance can reach out to LORD MEDUZA, as his work embodies what I term perfection. He can be contacted via
ReplyDeleteWHATSAPP: +1 807 907 2687
EMAIL: lordmeduzatemple@hotmail.com
Android classes online offer step-by-step app development practice. It explains Android architecture clearly. This android classes online improve technical understanding. It supports guided coding sessions. Students gain hands-on exposure. It is efficient.
ReplyDelete