The material is based on my workshop at Berkeley - Machine learning with scikit-learn. I convert it here so that there will be more explanation. Note that, the code is written using Python 3.6. It is better to read the slides I have first, which you can find it here. You can find the notebook on Qingkai's Github.

This week, we will discuss some common practices that we skipped in the previous weeks. These common practices will help us to train a model that generalize well, that is perform well on the new data that we want to predict.

from sklearn import datasets
import numpy as np
import matplotlib.pyplot as plt

plt.style.use('seaborn-poster')

%matplotlib inline

Classification Example

from sklearn.model_selection import train_test_split
from sklearn import metrics
from sklearn import preprocessing

#get the dataset
iris = datasets.load_iris()
X, y = iris.data, iris.target

# Split the dataset into a training and a testing set
# Test set will be the 25% taken randomly
X_train, X_test, y_train, y_test = train_test_split(X, y,
 test_size=0.25, random_state=33)
print(X_train.shape, y_train.shape)

(112, 4) (112,)

X_train[0]

array([ 5. ,  2.3,  3.3,  1. ])

Let's standardize the input features

# Standardize the features
scaler = preprocessing.StandardScaler().fit(X_train)
X_train = scaler.transform(X_train)
X_test = scaler.transform(X_test)

X_train[0]

array([-0.91090798, -1.59761476, -0.15438202, -0.14641523])

#Using svm
from sklearn.svm import SVC
clf = SVC()
clf.fit(X_train, y_train)

clf.score(X_test, y_test)

0.94736842105263153

Pipeline

We can use pipeline to chain all the operations into a simple pipeline:

from sklearn.pipeline import Pipeline

estimators = []
estimators.append(('standardize', preprocessing.StandardScaler()))
estimators.append(('svm', SVC()))
pipe = Pipeline(estimators)

pipe.fit(X_train, y_train)

pipe.score(X_test, y_test)

0.94736842105263153

When evaluating different settings (“hyperparameters”) for estimators, such as the C setting that must be manually set for an SVM, there is still a risk of overfitting on the test set because the parameters can be tweaked until the estimator performs optimally. This way, knowledge about the test set can “leak” into the model and evaluation metrics no longer report on generalization performance. To solve this problem, yet another part of the dataset can be held out as a so-called “validation set”: training proceeds on the training set, after which evaluation is done on the validation set, and when the experiment seems to be successful, final evaluation can be done on the test set. However, by partitioning the available data into three sets, we drastically reduce the number of samples which can be used for learning the model, and the results can depend on a particular random choice for the pair of (train, validation) sets. A solution to this problem is a procedure called cross-validation (CV for short). A test set should still be held out for final evaluation, but the validation set is no longer needed when doing CV. In the basic approach, called k-fold CV, the training set is split into k smaller sets (other approaches are described below, but generally follow the same principles). The following procedure is followed for each of the k “folds”: A model is trained using k-1 of the folds as training data; the resulting model is validated on the remaining part of the data (i.e., it is used as a test set to compute a performance measure such as accuracy). The performance measure reported by k-fold cross-validation is then the average of the values computed in the loop. This approach can be computationally expensive, but does not waste too much data (as it is the case when fixing an arbitrary test set), which is a major advantage in problem such as inverse inference where the number of samples is very small.

Computing cross-validated metrics

The simplest way to use cross-validation is to call the crossvalscore helper function on the estimator and the dataset.

from sklearn.model_selection import cross_val_score

scores = cross_val_score(pipe, X, y, cv=5)
scores

array([ 0.96666667,  0.96666667,  0.96666667,  0.93333333,  1.        ])

The mean score and the 95% confidence interval of the score estimate are hence given by:

print("Accuracy: %0.2f (+/- %0.2f)" % (scores.mean(), scores.std()))

Accuracy: 0.97 (+/- 0.02)

It is also possible to use other cross validation strategies by passing a cross validation iterator instead, for instance:

from sklearn.model_selection import ShuffleSplit
cv = ShuffleSplit(n_splits=3, test_size=0.3, random_state=0)

cross_val_score(pipe, iris.data, iris.target, cv=cv)

array([ 0.97777778,  0.93333333,  0.95555556])

Using cross-validation choose parameters

For example, if we want to test different value of C vlaues for the SVM, we can run the following code and decide the best parameter. We can have a look of all the parameters we used in our pipeline by using get_params function.

pipe.get_params()

{'standardize': StandardScaler(copy=True, with_mean=True, with_std=True),
 'standardize__copy': True,
 'standardize__with_mean': True,
 'standardize__with_std': True,
 'steps': [('standardize',
   StandardScaler(copy=True, with_mean=True, with_std=True)),
  ('svm', SVC(C=1.0, cache_size=200, class_weight=None, coef0=0.0,
     decision_function_shape=None, degree=3, gamma='auto', kernel='rbf',
     max_iter=-1, probability=False, random_state=None, shrinking=True,
     tol=0.001, verbose=False))],
 'svm': SVC(C=1.0, cache_size=200, class_weight=None, coef0=0.0,
   decision_function_shape=None, degree=3, gamma='auto', kernel='rbf',
   max_iter=-1, probability=False, random_state=None, shrinking=True,
   tol=0.001, verbose=False),
 'svm__C': 1.0,
 'svm__cache_size': 200,
 'svm__class_weight': None,
 'svm__coef0': 0.0,
 'svm__decision_function_shape': None,
 'svm__degree': 3,
 'svm__gamma': 'auto',
 'svm__kernel': 'rbf',
 'svm__max_iter': -1,
 'svm__probability': False,
 'svm__random_state': None,
 'svm__shrinking': True,
 'svm__tol': 0.001,
 'svm__verbose': False}

C_s = np.linspace(0.001, 1000, 100)

scores = list()
scores_std = list()
for C in C_s:
    pipe.set_params(svm__C = C)
    this_scores = cross_val_score(pipe, X, y, n_jobs=1, cv = 5)
    scores.append(np.mean(this_scores))
    scores_std.append(np.std(this_scores))

# Do the plotting
plt.figure(1, figsize=(10, 8))
plt.clf()
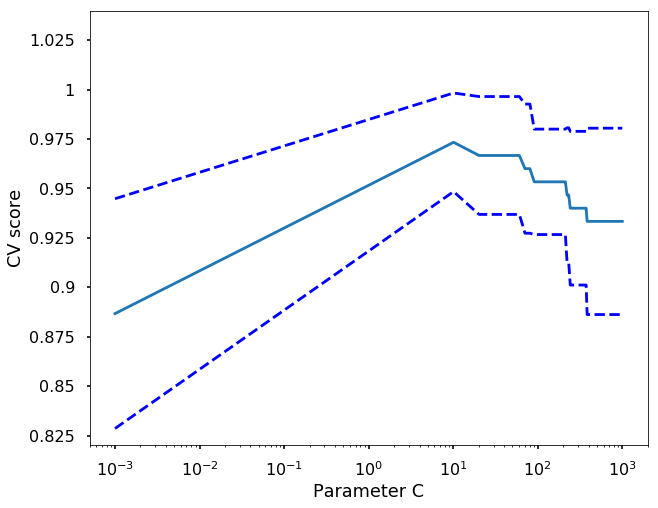
plt.semilogx(C_s, scores)
plt.semilogx(C_s, np.array(scores) + np.array(scores_std), 'b--')
plt.semilogx(C_s, np.array(scores) - np.array(scores_std), 'b--')
locs, labels = plt.yticks()
plt.yticks(locs, list(map(lambda x: "%g" % x, locs)))
plt.ylabel('CV score')
plt.xlabel('Parameter C')
plt.ylim(0.82, 1.04)
plt.show()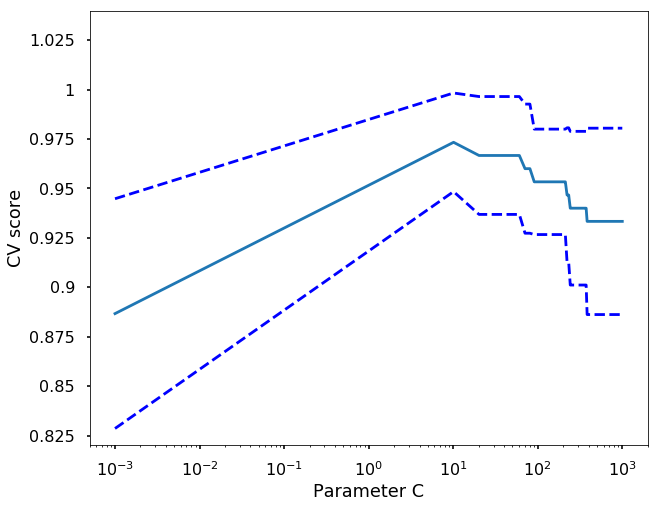

Alternatively, we can use the GridSearchCV to do the same thing:

from sklearn.model_selection import GridSearchCV

params = dict(svm__C=np.linspace(0.001, 1000, 100))

grid_search = GridSearchCV(estimator=pipe, param_grid=params,n_jobs=-1, cv=5)

grid_search.fit(X,y)

GridSearchCV(cv=5, error_score='raise',
       estimator=Pipeline(steps=[('standardize', StandardScaler(copy=True, with_mean=True, with_std=True)), ('svm', SVC(C=1000.0, cache_size=200, class_weight=None, coef0=0.0,
  decision_function_shape=None, degree=3, gamma='auto', kernel='rbf',
  max_iter=-1, probability=False, random_state=None, shrinking=True,
  tol=0.001, verbose=False))]),
       fit_params={}, iid=True, n_jobs=-1,
       param_grid={'svm__C': array([  1.00000e-03,   1.01020e+01, ...,   9.89899e+02,   1.00000e+03])},
       pre_dispatch='2*n_jobs', refit=True, return_train_score=True,
       scoring=None, verbose=0)

grid_search.best_score_

0.97333333333333338

grid_search.best_params_

{'svm__C': 10.102}

You can see all the results in grid_search.cv_results_

Exercise

Using the grid_search.cv_results_ from the GridSearchCV, plot the same figure as above which showing the parameter C vs. CV score.

# Do the plotting
plt.figure(1, figsize=(10, 8))
plt.clf()

C_s = grid_search.cv_results_['param_svm__C'].data
scores = grid_search.cv_results_['mean_test_score']
scores_std = grid_search.cv_results_['std_test_score']

plt.semilogx(C_s, scores)
plt.semilogx(C_s, np.array(scores) + np.array(scores_std), 'b--')
plt.semilogx(C_s, np.array(scores) - np.array(scores_std), 'b--')
locs, labels = plt.yticks()
plt.yticks(locs, list(map(lambda x: "%g" % x, locs)))
plt.ylabel('CV score')
plt.xlabel('Parameter C')
plt.ylim(0.82, 1.04)
plt.show()

This week, we will talk how to use scikit-learn for unsupervised learning, we will talk one example in dimensionality reduction and one in clustering.

Unsupervised learning

Unsupervised Learning addresses a different sort of problem. Here the data has no labels, and we are interested in finding similarities between the objects in question. In a sense, you can think of unsupervised learning as a means of discovering labels from the data itself.

Unsupervised learning comprises tasks such as dimensionality reduction, clustering, and density estimation. For example, in the iris data discussed before, we can use unsupervised methods to determine combinations of the measurements which best display the structure of the data. As we'll see below, such a projection of the data can be used to visualize the four-dimensional dataset in two dimensions.

Dimensionality reduction with PCA

Principle Component Analysis (PCA) is a dimension reduction technique that can find the combinations of variables that explain the most variance. Consider the iris dataset. It cannot be visualized in a single 2D plot, as it has 4 features. We are going to extract 2 combinations of sepal and petal dimensions to visualize it:

from sklearn import datasets
import numpy as np
import matplotlib.pyplot as plt

plt.style.use('seaborn-poster')
%matplotlib inline

iris = datasets.load_iris()
X = iris.data
print("The dataset shape:", X.shape)

X, y = iris.data, iris.target

The dataset shape: (150, 4)

Use PCA, we can reduce the dimensions from 4 into 2 and visualize it.

from sklearn.decomposition import PCA

pca = PCA(n_components=2)
pca.fit(X)
X_reduced = pca.transform(X)
print("Reduced dataset shape:", X_reduced.shape)

Reduced dataset shape: (150, 2)

plt.figure(figsize=(10,8))
plt.scatter(X_reduced[:, 0], X_reduced[:, 1], c=y, cmap='RdYlBu')
plt.xlabel('First component')
plt.ylabel('Second component')

<matplotlib.text.Text at 0x1129a3cf8>

Clustering with K-means

K Means is an algorithm for unsupervised clustering: that is, finding clusters in data based on the data attributes alone (not the labels).

K Means is a relatively easy-to-understand algorithm. It searches for cluster centers which are the mean of the points within them, such that every point is closest to the cluster center it is assigned to.

Let's look at how KMeans operates on the simple clusters we looked at previously - The Iris dataset. To emphasize that this is unsupervised, we'll not plot the colors of the clusters:

Train K-means

from sklearn.cluster import KMeans

k_means = KMeans(n_clusters=3, random_state=2)
k_means.fit(X)
y_pred = k_means.predict(X)

plt.figure(figsize=(10,8))
plt.scatter(X_reduced[:, 0], X_reduced[:, 1], c=y_pred, cmap='RdYlBu')
plt.xlabel('First component')
plt.ylabel('Second component')

<matplotlib.text.Text at 0x112ec65c0>

Excercise

When we use PCA, visualization is just one purpose. Sometimes, we have high dimensional data that we want to use PCA to reduce the dimensionality while keep certain amount of information in the new PCA transformed data.

In this exercise, please use PCA on the Iris data and keep the components that explained 95% of the variance of the original data.

############################### Solution 1 #################################

# fit a PCA model
pca = PCA().fit(X)

plt.figure(figsize=(10,8))
plt.plot(range(1, X.shape[1]+1), np.cumsum(pca.explained_variance_ratio_))
plt.xlabel('number of components')
plt.ylabel('cumulative explained variance')

# we can see that with the first two components, we can explain over 95% of the variance, 
# then we can train PCA with only 2 components
# fit a PCA model
pca = PCA(n_components = 2).fit(X)
X_reduced = pca.transform(X)

############################### Solution 2 #################################
## Or we can simplely use n_components = 0.95
pca = PCA(n_components = 0.95).fit(X)
X_reduced = pca.transform(X)

Qingkai's Blog

Saturday, July 29, 2017

Machine learning 17: Using scikit-learn Part 5 - Common practices