Wife's painting: Paintings from my wife

This week, I will just show some of my wife's paintings here. She loves painting and wants to become an architect. I hope she can be a happy architect in the future. I am so proud of my wife! You can check out all my wife's paintings.

Earthquake on egg shell

We three

Shower

Church at Berkeley

Grace cathedral

Mother and Child (Picasso)

Father and Daughter

Faceless self-portrait

self-portrait (1 to 1 ratio)

My family

Signal processing: How autocorrelation works (animation example)

As promised last week, this week, we will show a simple example - how autocorrelation works. I tried to find a nice animation online, but I can not find it. Therefore, this week, let's just create a simple movie of showing how autocorrelation works. You can find all the code at Qingkai's Github. 

from statsmodels import api as sm
import matplotlib.pyplot as plt
import numpy as np
import matplotlib.animation as manimation

plt.style.use('seaborn-poster')
%matplotlib inline

Generate a sine signal

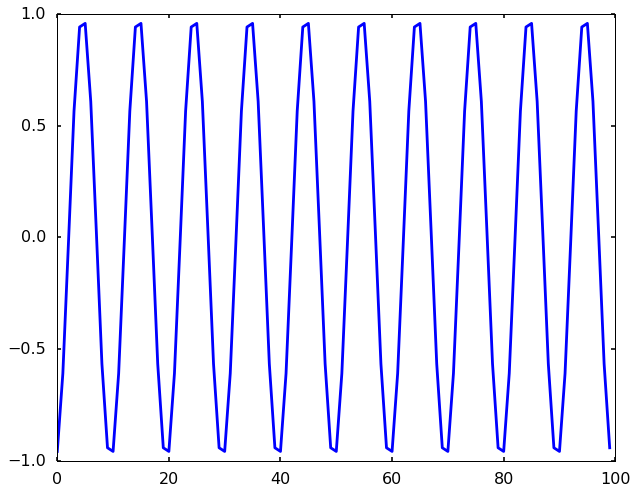
Let's first generate a sine wave with frequency 0.1 Hz, and we can sample it sampling rate 1 Hz. We can plot the figure as showing below:

Fs = 1  # sampling rate
Ts = 1.0/Fs # sampling interval
t = np.arange(0,100,Ts) # time vector
ff = 0.1;   # frequency of the signal
# create the signal
y = np.sin(2*np.pi*ff*t + 5)

plt.figure(figsize = (10, 8))
plt.plot(t, y)
plt.show()

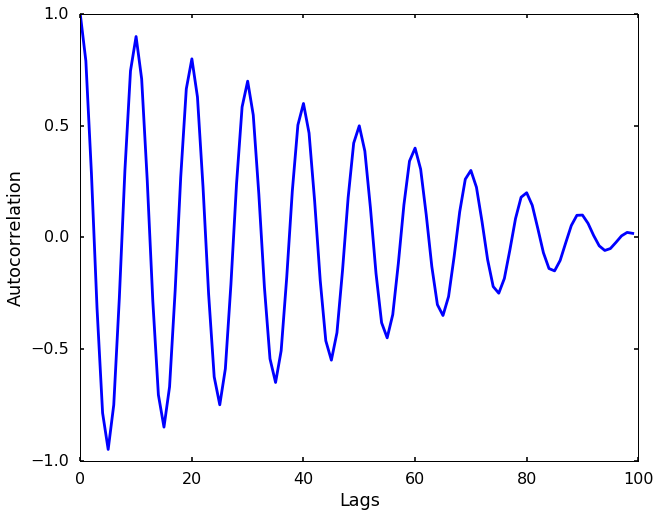
Plot the autocorrelation using statsmodels

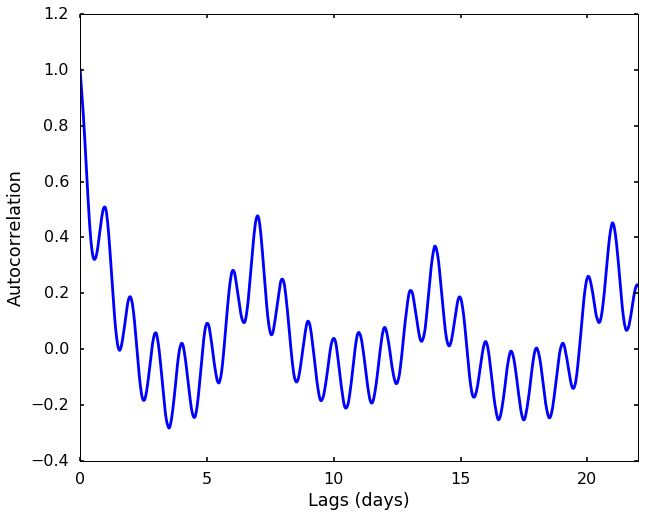
We can first plot the autocorrelation using an existing package - statsmodels. The idea of autocorrelation is to provide a measure of similarity between a signal and itself at a given lag. We can see the following figure. Maybe you think it is hard to understand from text description, let's create an animation in the next section to reproduce this figure, and hope you will have a better understand there. 

# get the autocorrelation coefficient
acf = sm.tsa.acf(y, nlags=len(y))

plt.figure(figsize = (10, 8))
lag = np.arange(len(y))
plt.plot(lag, acf)
plt.xlabel('Lags')
plt.ylabel('Autocorrelation')

Let's make a simple movie to show how it works

In this section, we will reproduce the above figure and make a simple animation to show how it works. As we talked last time, it is a simple method in the time domain that you shift the signal with a time lag and calculate the correlation with the original signal (or we can simply multiply the two signals to get a number, and then we can divide the largest number to scale the value to -1 to 1). We can use the functions we talked before to shift the signal in the frequency domain as shown in the following cell. 

def nextpow2(i):
    '''
    Find the next power 2 number for FFT
    '''
    
    n = 1
    while n < i: n *= 2
    return n

def shift_signal_in_frequency_domain(datin, shift):
    '''
    This is function to shift a signal in frequency domain. 
    The idea is in the frequency domain, 
    we just multiply the signal with the phase shift. 
    '''
    Nin = len(datin) 
    
    # get the next power 2 number for fft
    N = nextpow2(Nin +np.max(np.abs(shift)))
    
    # do the fft
    fdatin = np.fft.fft(datin, N)
    
    # get the phase shift for the signal, shift here is D in the above explaination
    ik = np.array([2j*np.pi*k for k in xrange(0, N)]) / N 
    fshift = np.exp(-ik*shift)
        
    # multiple the signal with the shift and transform it back to time domain
    datout = np.real(np.fft.ifft(fshift * fdatin))
    
    # only get the data have the same length as the input signal
    datout = datout[0:Nin]
    
    return datout

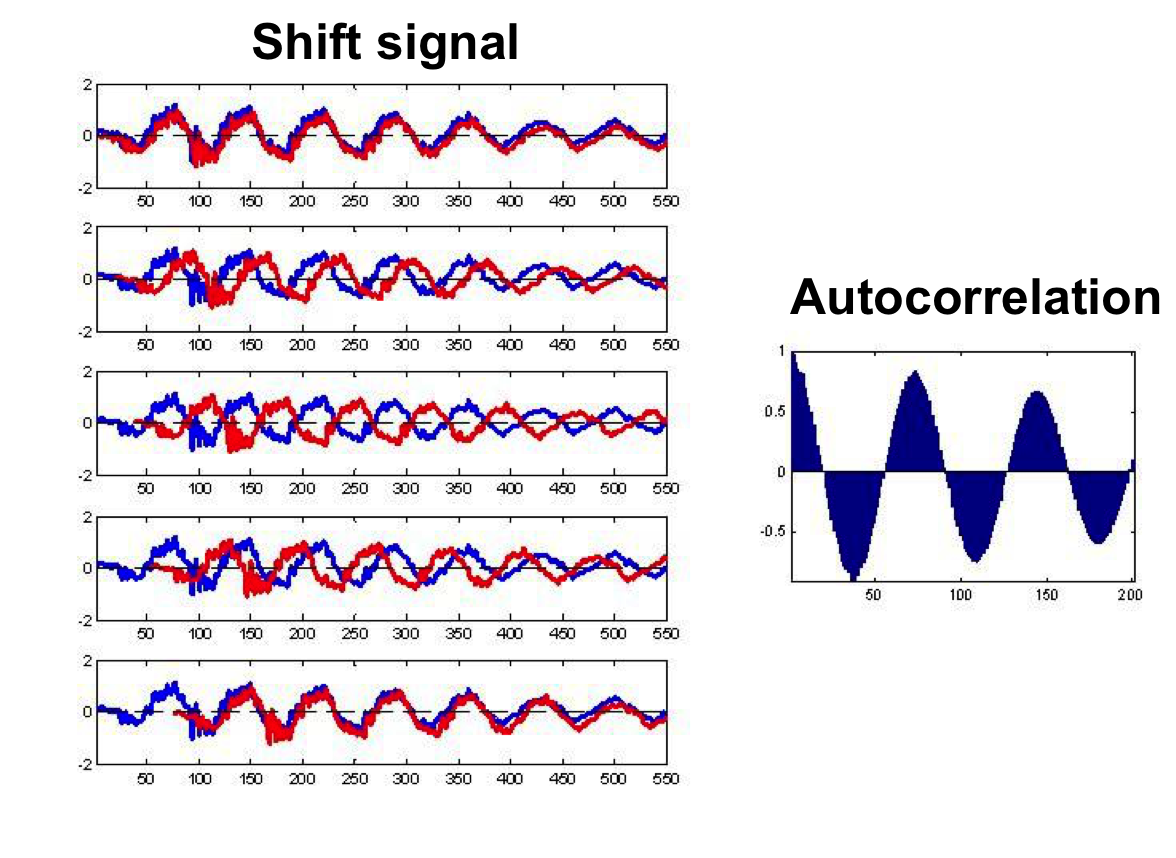
Let's make the movie below. We will shift the signal 1 at a step, and calculate a simple correlation normalized by the largest value (the two signals overlap with each other, or 0 lag). 

FFMpegWriter = manimation.writers['ffmpeg']
metadata = dict(title='Movie Test', artist='Matplotlib',
                comment='Movie support!')
writer = FFMpegWriter(fps=15, metadata=metadata)

lags = []
acfs = []
norm = np.dot(y, y)
fig = plt.figure(figsize = (10, 8))
n_frame = len(y)

def updatefig(i):
    '''
    a simple helper function to plot the two figures we need, 
    the top panel is the time domain signal with the red signal
    showing the shifted signal. The bottom figure is the one
    corresponding to the autocorrelation from the above figure. 
    '''
    fig.clear()
    # shift signal
    y_shift = shift_signal_in_frequency_domain(y, i)
    plt.subplot(211)
    plt.plot(t, y, 'b')
    plt.plot(t, y_shift, 'r')
    plt.ylabel('Amplitude')
    plt.title('Lag: ' + str(i))

    plt.subplot(212)
    # get the lag
    lags.append(i)
    # simple way to calculate autocorrelation
    acf = np.dot(y_shift, y)
    # add to the list with normalized value. 
    acfs.append(acf/norm)
    plt.plot(lags, acfs)
    plt.xlabel('Lags')
    plt.ylabel('Autocorrelation')
    plt.xlim(0, n_frame)
    plt.ylim(-1, 1)
    plt.draw()

# save the movie to file
anim = manimation.FuncAnimation(fig, updatefig, n_frame)
anim.save("./autocorrelation_example.mp4", fps=10, dpi = 300)

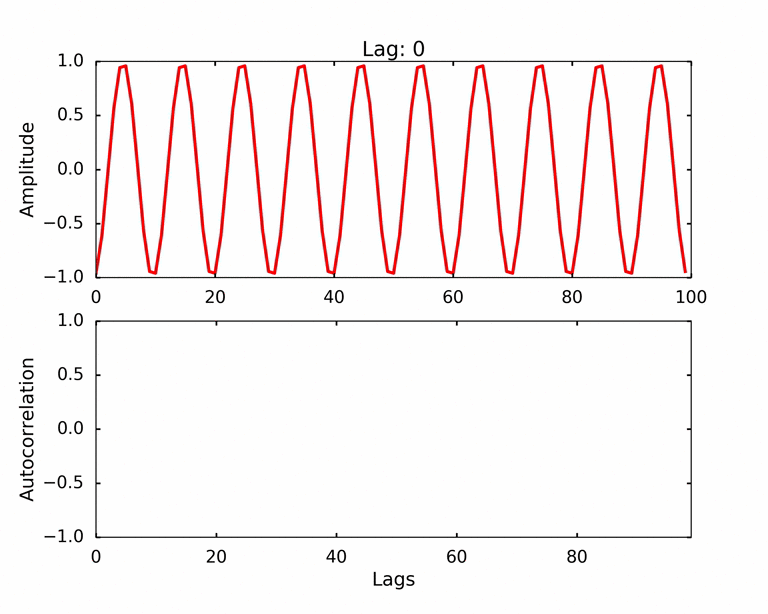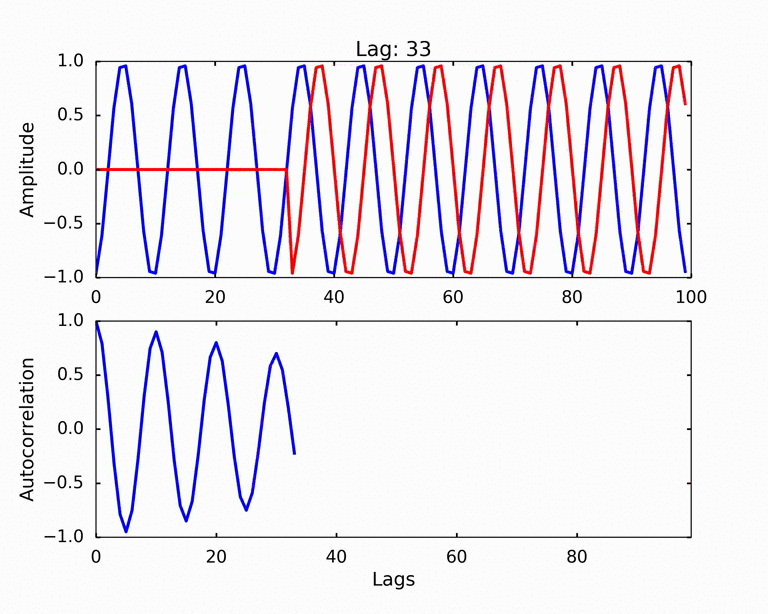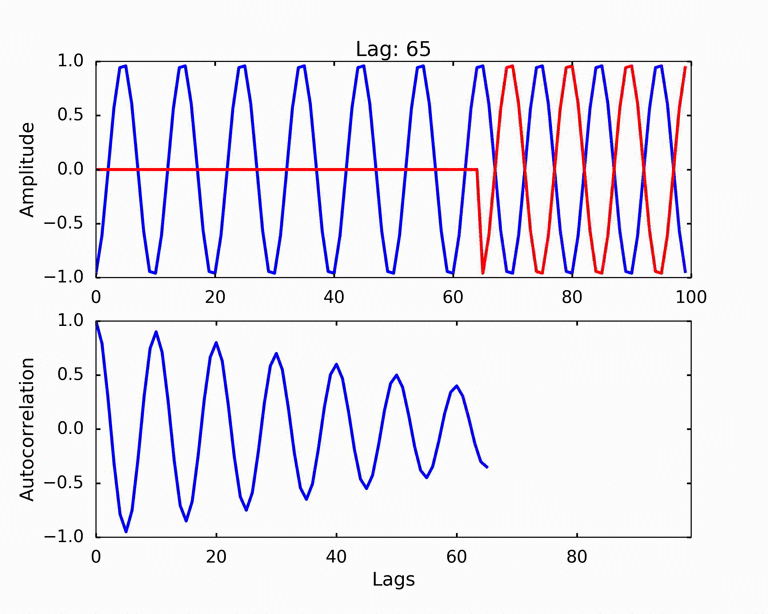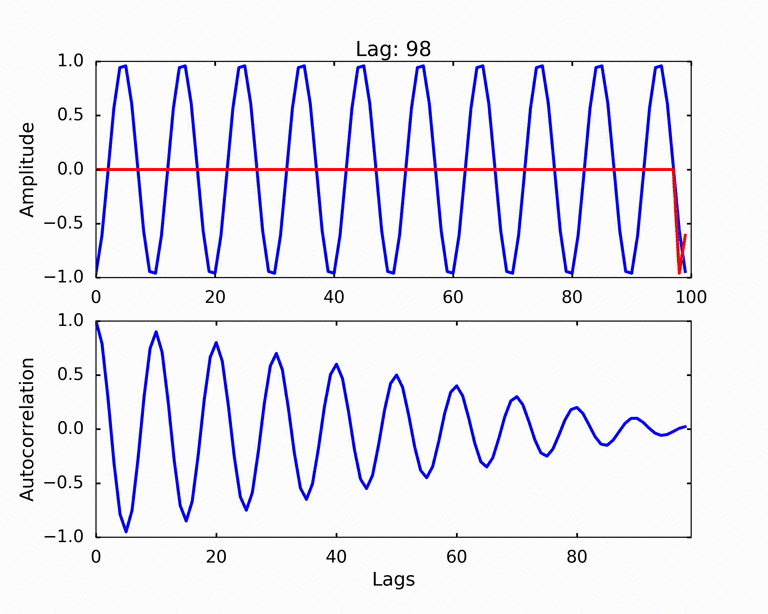
We can now have a much better view of how autocorrelation works. We shift the signal by 1 at a time, and calculate the autocorrelation as the following steps: 1. multiply the numbers from two signals at each timestamp (You can think two signals as two arrays, and we do an elementwise multiply of the two arrays) 2. after the elementwise multiplication, we get another array, which we will sum them up and divide the normalization factor to get a number - the autocorrelation. The normalization factor is the largest autocorrelation number we can get, which is the autocorrelation when the signal has 0 lag. 

This is basically the dot product of the two signals. We can see as the red signal shifted away from the very beginning of the total overlap, the two signals start to out of phase, and the autocorrelation decreasing. Due to the signal is a periodic signal, the red signal soon overlap with the blue signal again. But we can see as the red signal shifted certain lags, it only partially overlap with the original blue signal, therefore, the autocorrelation of the 2nd peak is smaller than the first peak. As the red signal shifted further, the part overlap becomes smaller, which generating the decreasing trend of the peaks. 

I hope now you have a better understanding how the autocorrelation works!

PS: I use the following command to convert mp4 to gif if you want to do the same thing

ffmpeg -i autocorrelation_example.mp4 -vf scale=768:-1 -r 10 -f image2pipe -vcodec ppm - | convert -delay 10 -loop 0 - output.gif

Signal processing: Finding periodic signal in time series data

This week, let's see a simple example how we can detect the periodic signals within the data. This is usually a quite interesting problem in many cases. Here, we will use a simple example from the readings of a thermometer in an office building. The thermometer measures the inside temperature every half hour for four months in Fahrenheit. Our goal is to find the periodic signal within it, that is when some pattern in the signal repeat. You can find the scripts on Qingkai's Github. 

Let's first load the data from the mat file. 

import scipy.io as sio
import numpy as np
import matplotlib.pyplot as plt
from scipy import fft, arange, signal
plt.style.use('seaborn-poster')
%matplotlib inline

# load the data
data = sio.loadmat('./data/officetemp.mat')

# convert to numpy array
temp = np.array([x[0] for x in data['temp']])

# convert the temp from Fahrenheit to Celsius
tempC = (temp - 32.)*5./9.

# we remove the mean of the signal to create a signal oscillating around 0
tempNorm = tempC - np.mean(tempC)

Since the data measured every half hour, we can either work in hours or days. I like to work in days, and the sampling rate is thus 2 measurements/hour × 24 hours/day = 48 measurements/day. Then we can create the timestamp for each measurement, and plot the data. 

# this is sampling rate, 48 samples/day
fs = 2*24

# create timestamp that start with 1, this is means
# our day start with day 1. 
t = arange(len(temp))/float(fs) + 1

# let's plot the data
plt.figure(figsize = (10, 8))
plt.plot(t, tempNorm)
plt.xlabel('Time (day)')
plt.ylabel('Temperature (degree)')

From the above figure, we can see the signal does seem to have some pattern repeat, but we can not tell how it repeat. This is actually our main goal: to get the period of the repeating signals. Let's first see a simple method, which is called zero crossings. It is a very simple way to estimate the frequency by counting the number of times the signal across the baseline, in this case 0, since we removed the mean of the signal. Then we can get a sense how the signal repeat. This technique is very simple and inexpensive but is not very accurate. It is mostly used to get a rough fundamental frequency of the signal. 

Zero crossings

from matplotlib.mlab import find
def freq_zero_crossing(sig, fs):
    """
    Frequency estimation from zero crossing method
    sig - input signal
    fs - sampling rate
    
    return: 
    dominant period
    """
    # Find the indices where there's a crossing
    indices = find((sig[1:] >= 0) & (sig[:-1] < 0))

    # Let's calculate the real crossings by interpolate
    crossings = [i - sig[i] / (sig[i+1] - sig[i]) for i in indices]
    
    # Let's get the time between each crossing
    # the diff function will get how many samples between each crossing
    # we divide the sampling rate to get the time between them
    delta_t = np.diff(crossings) / fs
    
    # Get the mean value for the period
    period = np.mean(delta_t)
    
    return period

period_from_zero_crossing = freq_zero_crossing(tempNorm, fs)
print('The period estimation is %.1f days'%(period_from_zero_crossing))

The period estimation is 1.4 days

We can see the estimation we got from the zero crossings is not so good, it is even difficult to explain why there is a signal repeating every 1.4 days. Well, this is just a rough estimation, and let's use a more popular and accurate method to estimate it - Fourier Transform. We use the periodogram from scipy to get the spectrum of the signal below. and plot the results. 

Frequency content

# get the frequency and spectrum
f, Pxx = signal.periodogram(tempNorm, fs = fs, window='hanning', scaling='spectrum')

plt.figure(figsize = (10, 8))
plt.plot(f, Pxx)
plt.xlim(0, 10)
plt.yscale('log')
plt.xlabel('Frequency (cycles/day)')
plt.ylabel('Spectrum Amplitude')

From the spectrum, we can see some peaks, and the corresponding frequency to each peak indicates the periodic signals, and how strong this frequency signal is showing in the spectrum amplitude. The higher the peak, the stronger of this signal repeating itself. Let's print out the top 5 peaks, and see how many days corresponding to them. After we got these peaks, we need interpret the results. We can see the 7 day peak is the strongest peak, which means for every 7 days the signal will repeat. 1 day peak is also very strong, there are two peaks associated with it, this is due to the leakage of the spectrum that we talked before in the taper blog. The 116 day is about the total length of the signal, and the 3.5 days is the half week. All these peaks seem correct, and can be explained using common sense. 

# print the top 6 period in the signal
for amp_arg in np.argsort(np.abs(Pxx))[::-1][1:6]:
    day = 1 / f[amp_arg]
    print(day)

7.27083333333
1.00287356322
0.994301994302
116.333333333
3.52525252525

Autocorrelation

Another common method to detect the periodic signal is to use autocorrelation. This is a simple method in the time domain that you shift the signal with a time lag and calculate the correlation with the original signal (or we can simply add the two signal up to get a number, and then we can divide the largest number to scale the value to -1 to 1). If there are any periodic signal, after certain time lag, we should see the correlation have a significant increase, and a simple example is shown in the following picture. On the left, we shift the same signal to the right (shown as the red signal), and on the right, it is the autocorrelation we calculate. We notice that the autocorrelation have a downward ramp, since the number of points added together to produce the value are reduced at each successive shift. The peaks in the autocorrelation figure are showing the periodic signal and its corresponding time lag (that is how much we shift the signal to get this correlation). Let's try to create an animation next week to show how autocorrelation works ^{)^}

from statsmodels import api as sm

# get the autocorrelation coefficient
acf = sm.tsa.acf(tempNorm, nlags=len(tempNorm))

plt.figure(figsize = (10, 8))
lag = arange(len(tempNorm)) / 2. / 24.
plt.plot(lag, acf)
plt.xlim((0, 120))
plt.xlabel('Lags (days)')
plt.ylabel('Autocorrelation')

plt.figure(figsize = (10, 8))
plt.plot(lag, acf)
plt.xlim((0, 22))
plt.xlabel('Lags (days)')
plt.ylabel('Autocorrelation')

From the two autocorrelation figures, we can see the clearest peaks are at 1 day, 7 days, 14 days, 21 days, ... Therefore, 1 day and 7 days are the periods of the repeating signals in the data. 

There are also many other methods to identify the periodic signals in the data, and we will add them in the future. 

References

https://www.mathworks.com/examples/signal/mw/signal-ex69123038-find-periodicity-using-autocorrelation https://www.mathworks.com/examples/signal/mw/signal-ex50284156-find-periodicity-using-frequency-analysis